Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Třinecko - Mostecko Jablunkovská funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 10. 2008 15:50 — Editoval Pavel (17. 10. 2008 15:55)
Třinecko - Mostecko Jablunkovská funkce
Najděte funkci  , která je definovaná na
, která je definovaná na 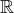 a splňuje následující podmínky:
a splňuje následující podmínky:
1.  není monotonní na žádném intervalu
není monotonní na žádném intervalu 
2.  je prostá na
je prostá na 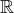
3. jednostranné limity funkce  neexistují v žádném reálném čísle
neexistují v žádném reálném čísle
4. existují vlastní limity 
5. v bodě  má
má  globální minimum a platí
globální minimum a platí 
Velde funkce  zkonstruujte funkci inverzní
zkonstruujte funkci inverzní 
![kopírovat do textarea $ \blue \mathbf{ \stackrel{\cdot\hspace{1pt}\rule[-8pt]{1pt}{10pt}\hspace{1pt}\cdot}{\smile}} $](/mathtex/30/30f364c154e87b7d13ef3aac746da38b.gif)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#2 17. 10. 2008 16:36
Re: Třinecko - Mostecko Jablunkovská funkce
↑ Pavel: Coz takhle trosku zacvicit s funkci atan, treba nasledovne:
pro x>=0, x racionalni: y = atan(x)
pro x>=0, x neracionalni: y = pi - atan(x)
pro x < 0, x racionalni: y = 2pi + atan(x)
pro x < 0, x neracionalni: y = pi - atan(x)
Dokonce by zapis sel i zjednodusit, ale nebylo by videt, jak jsem to konstruoval. Inverzni funkce by se popsala analogicky. Splnuje to vsechno?
Offline
#3 17. 10. 2008 17:16
Re: Třinecko - Mostecko Jablunkovská funkce
↑ musixx:
Je to tak, pěkné řešení.
Funkce č.2:
Najděte funkci  , která je definovaná na
, která je definovaná na 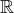 a splňuje následující podmínky:
a splňuje následující podmínky:
1. v bodě  má
má  globální minimum a platí
globální minimum a platí 
2.  je diferencovatelná na libovolném prstencovém okolí bodu
je diferencovatelná na libovolném prstencovém okolí bodu 
3.  není funkce
není funkce  monotonní na intervalech
monotonní na intervalech  a
a 
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 17. 10. 2008 22:21 — Editoval BrozekP (17. 10. 2008 22:21)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Třinecko - Mostecko Jablunkovská funkce
↑ Pavel:
Co třeba funkce
dodefinovaná v nule hodnotou 0?
Offline
#5 17. 10. 2008 22:39 — Editoval BrozekP (18. 10. 2008 00:57)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Třinecko - Mostecko Jablunkovská funkce
Zajímavé by mohlo být hledat funkci  (definovanou pro všechna reálná čísla), která má limitu nekonečno
(definovanou pro všechna reálná čísla), která má limitu nekonečno
a) ve spočetně mnoha bodech
b) ve všech racionálních bodech
c) ve všech bodech
d) na množině bodů, která má nenulovou jednorozměrnou Lebesgueovu míru
Případ a) je taková rozcvička. Případy b), c), d) jsem nerozmýšlel, takže je možné, že jsou triviální :-)
Offline
#6 20. 10. 2008 19:08
Re: Třinecko - Mostecko Jablunkovská funkce
↑ BrozekP:
ad a) 
ad b) pokud má taková funkce existovat, pak pro libovolné racionální číslo existuje okolí  takové, že funkční hodnota ve všechn reálných číslech náležící do tohoto okolí je větší než libovolná předem daná kladná konstanta. A tedy pro každé iracionální číslo spadající do okolí
takové, že funkční hodnota ve všechn reálných číslech náležící do tohoto okolí je větší než libovolná předem daná kladná konstanta. A tedy pro každé iracionální číslo spadající do okolí  existuje okolí
existuje okolí  takové, že platí totéž. A tak funkce nabývá nekonečné hodnoty pro všechna reálná čísla.
takové, že platí totéž. A tak funkce nabývá nekonečné hodnoty pro všechna reálná čísla.
Chce to hodně silný dalekohled, abychom se na tu funkci podívali blíž :-)
ad c), d) totéž
Kdybychom zeslabili požadavek tak, aby limes superior byl nekonečný, pak by bylo myslím možné nějakou rozumnou funkci najít.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 21. 10. 2008 16:55 — Editoval BrozekP (21. 10. 2008 17:30)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Třinecko - Mostecko Jablunkovská funkce
↑ Pavel:
Stále si tvůj důkaz procházím a stále mi není zřejmé, že by byl úplný. Ukázal jsi, že existuje nějaká množina V (závislá na K), v které jsou funkční hodnoty větší než K. Ale ta množina V je právě závislá na K, nemůžeš pro každé K vzít stejnou množinu V. V tom vidím ten problém.
Já bych zkusil důkaz spíše způsobem, že bych pro každé pevné reálné x a K přímo dokázal, že f(x)>K. Bohužel zatím nevím jak. Symbolicky by se to dalo zapsat:
Offline
#8 22. 10. 2008 19:04 — Editoval Pavel (22. 10. 2008 19:04)
Re: Třinecko - Mostecko Jablunkovská funkce
↑ BrozekP:
Co to dokázat takto?
Nech?  je iracionální číslo. Protože množina racionálních čísel je hustá v
je iracionální číslo. Protože množina racionálních čísel je hustá v 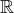 , existuje posloupnost racionálních čísel
, existuje posloupnost racionálních čísel  , která konverguje k číslu
, která konverguje k číslu  . Pro každý člen posloupnosti
. Pro každý člen posloupnosti  definujme okolí
definujme okolí
Protože má funkce  podle předpokladu nekonečnou limitu ve všech racionálních číslech (tedy i ve členech posloupnosti
podle předpokladu nekonečnou limitu ve všech racionálních číslech (tedy i ve členech posloupnosti  ), musí platit, že
), musí platit, že 
Jenže posloupnost  konverguje k iracionálnímu číslu
konverguje k iracionálnímu číslu  . A tak
. A tak
Takže funkce  nabývá v iracionálním čísle
nabývá v iracionálním čísle  libovolně velké hodnoty.
libovolně velké hodnoty.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 23. 10. 2008 10:23
Re: Třinecko - Mostecko Jablunkovská funkce
↑ Pavel:
Je zvláštní reagovat na svůj vlastní příspěvek, ale asi tam mám chybu. Ta okolí se mohou "zmenšovat" rychleji, než je "rychlost" konvergence posloupnosti  . Takže se může stát, že to
. Takže se může stát, že to  nemusí náležet žádnému z těchto okolí.
nemusí náležet žádnému z těchto okolí.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#10 23. 10. 2008 15:12
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Třinecko - Mostecko Jablunkovská funkce
↑ Pavel:
Ano, přesně na tenhle problém jsem také narazil. Je to těžší, než se zdá. Skoro začínám uvažovat, jestli by funkce splňující b) přeci jen nemohla existovat :-)
Offline
#11 28. 10. 2008 12:50 — Editoval BrozekP (28. 10. 2008 12:52)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Třinecko - Mostecko Jablunkovská funkce
Jenom takový nápad:
Pro racionální čísla  , p a q nesoudělná definujeme funkci
, p a q nesoudělná definujeme funkci
,
To by zaručilo, že pro každé racionální číslo bude limita nekonečno. Nevím ale, jestli suma v každém iracionálním čísle konverguje, to by chtělo ukázat, případně najít lepší funkci do sumy (jestli taková existuje).
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Třinecko - Mostecko Jablunkovská funkce (TOTO TÉMA JE VYŘEŠENÉ)