Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » rovnice se separovanými proměnnými (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 06. 2012 19:50
rovnice se separovanými proměnnými
Dobrý den...Po integraci rovnice dostanu: ln/y/=x - ln/x+1/ +C ..... další úpravou bych měla dostat: ln/y/=ln  - ln /x+1/ + ln K ....... jak vím, že to x je logaritmus ln
- ln /x+1/ + ln K ....... jak vím, že to x je logaritmus ln  ?? a podle čeho to pak upravím na: ln/y/= ln K
?? a podle čeho to pak upravím na: ln/y/= ln K  děleno / x+1/ ? a jak to pak odlogaritmuju? Dííky:-)
děleno / x+1/ ? a jak to pak odlogaritmuju? Dííky:-)
Offline
- (téma jako vyřešené označil(a) Popelína)
#2 06. 06. 2012 19:58
Re: rovnice se separovanými proměnnými
A ještě: 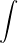 dy/4y-1 =
dy/4y-1 = 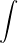 dx/x po integraci by mělo vyjít: 1/4 ln /4y-1/=ln/x/ + lnK ....1/4 mám před logaritmem asi proto, že jsem ji vytkla, ale proč je tedy v absolutní hodnotě pořád čtverka? ..... a Jak jsem pak z toho hostala ln/4y-1/=ln K^4 x^4 ? děkuju
dx/x po integraci by mělo vyjít: 1/4 ln /4y-1/=ln/x/ + lnK ....1/4 mám před logaritmem asi proto, že jsem ji vytkla, ale proč je tedy v absolutní hodnotě pořád čtverka? ..... a Jak jsem pak z toho hostala ln/4y-1/=ln K^4 x^4 ? děkuju
Offline
#3 07. 06. 2012 08:20 — Editoval chipák (07. 06. 2012 08:44)
Re: rovnice se separovanými proměnnými
↑ Popelína:
No veznu to postupně:
- Jak vím, že to je logaritmus  ?
?
Plyne to z definice funkcí logaritmu a  . Například
. Například  .
.
- a podle čeho to pak upravím na: ln/y/= ln K děleno / x+1/ ? a jak to pak odlogaritmuju?
Vzorce pro počítání s logaritmy. Odkaz Odlogaritmovat to můžeš, když máš na každé straně jeden logaritmus, prostě pokud se mají rovnat logaritmy, musí se rovnat jejich argumenty (škrtneš logaritmus).
- k poslednímu příspěvku:
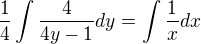
Teď máš v čitateli těch zlomků derivaci jmenovatele, tzn že integrál těch výrazů bude logaritmus absolutní hodnoty jmenovatele.

- a Jak jsem pak z toho hostala ln/4y-1/=ln K^4 x^4 ?
4ka jde do exponentu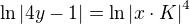
Offline
#5 07. 06. 2012 15:03
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnice se separovanými proměnnými
↑ Popelína:
Zdravím,
co míníš sdělením:
Popelína napsal(a):
ještě : dy/dx= y
2
nastuduj, prosím, pravidla pro matematické zápisy a řádně používej. Pokud potřebuješ pomoc se zápisem, zeptej se tady. Také v jednom tématu řeš pouze jeden problém - viz pravidla. Děkuji za pochopení.
↑ chipák:
děkuji.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » rovnice se separovanými proměnnými (TOTO TÉMA JE VYŘEŠENÉ)

