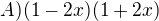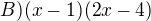Skrytý text:Příklad 1)Pro

upravte:
 Příklad 2)
Příklad 2)Pro

řešte:
 Příklad 3)
Příklad 3)Pro

řešte:
 Příklad 4-6
Příklad 4-6První dva členy aritmetické posloupnosti jsou
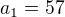

4) Vypočítejte padesátý člen
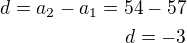

5) Vypočtěte součet prvních 50-ti členů posloupnosti:

6) Kolik prvních členů posloupnosti je třeba sečíst, aby byl součet co největší?
Protože první člen je 57 (dělitelné 3) a diference je d= -3 potom bude existovat člen
jehož hodnota je rovna nule .Další člen už bude záporný tj. součet se bude snižovat.
Bude platit:

Je tedy potřeba sečíst 20 členů posloupnosti.
Protože však 20-tý člen =0 potom nám stačí sečíst i 19 členů jelikož 20-tý člen nemá na součet vliv
Odpověď je tedy : 19 nebo 20 členů
Příklad 7)Graf nepřímé úměrnosti s předpisem

kde

, prochází bodem
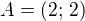
7.1 Vypočtěte konstantu k

7.2 Vypočtěte souřadnici x bodu

a souřadnici y bodu

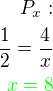
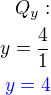 Příklad 8-9
Příklad 8-9Rovnoběžné přímky p, q protínají přímku r v bodech P; Q.
Vzdálenost rovnoběžek je 5 cm. Odchylka přímek p, r = 30 stupňů.
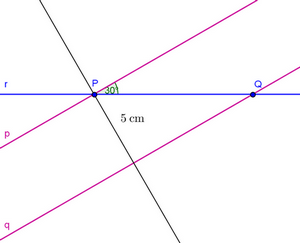
8) Určete vzdálenost bodu P od přímky q
Protože bod P leží na přímce p a vzdálenost rovnoběžek p, q je dle zadání 5 cm,
potom i vzdálenost bodu P od přímky q je 5 cm
9) Vypočtěte vzdálenost bodů P a Q
Platí:
 Příklad 10)
Příklad 10)Velikost vnitřních úhlů trojúhelníku ABC jsou


Vypočtěte velikost třetího úhlu
Součet vnitřních úhlů trojúhelníka je

tedy hledaný úhel bude:
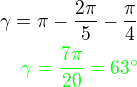 Příklad 11)
Příklad 11)V rovině je dána přímka q

Zapište obecnou rovnici přímky p, která prochází bodem

a je kolmá k přímce q
Kolmá přímka k přímce q

bude mít tvar:

dosazením souřadnic bodu A do předpisu dopočteme c
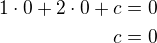
Rovnice přímky p:
 Příklad 12)
Příklad 12)Hmotnostní procento zlata ve slitině je přímo úměrná počtu karátů.
Slitina obsahující 75 % zlata se označuje 18-ti karáty.
Kolik procent zlata obsahuje 24 karátový prsten?

procent
Příklad 13)Cesta do školy je dlouhá 10 km a na kole se ujede za půl hodiny.
Stejná cesta zpět trvá o 10 minut déle.
O kolik km/h se liší průměrná rychlost na cestě tam a zpět?
Průměrná rychlost při cestě tam:

Průměrná rychlost při cestě zpět

Rozdíl:
 Příklad 14)
Příklad 14)Z pečlivě promíchaného balíčku 52 karet bylo odebráno 7 karet.
Mezi zbývajícími kartami zůstává 9 srdcových karet.
Jaká je pravděpodobnost, že v dalším tahu z balíku karet
nebude vytažena srdcová karta?
V balíku zůstává 45 karet (52-7)
9 z nich je srdcových
Pravděpodobnost, že při tahu jedné karty vytáhnu srdcovou je

Že tuto kartu nevytáhnu je jev opačný tedy pravděpodobnost, že karta nebude vytažena je:
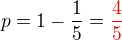
2. řešení:
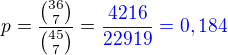 Příklad 15)
Příklad 15)Kvádr se čtvercovou podstavou má výšku x cm. Podstavná hrana je
o 3 cm kratší než dvojnásobek výšky kvádru.
Napište vztah pro výpočet objemu kvádru v závislosti na x. Upravte jej do tvaru mnohočlenu
Objem kváru bude



cm^3
Příklad 16)Trojúhelník má vrcholy v bodech


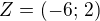
Trojúhelník narýsujte a rozhodněte o každém následujích tvrzení:
16.1 Trojúhelník je rovnoramenný
16.2 Trojúhelník je ostroúhlý
16.3 Pata výšky spuštěná z bodu X se shoduje se středem strany YZ
16.4 Pata výšky spuštěná z bodu Z se shoduje se středem strany XY
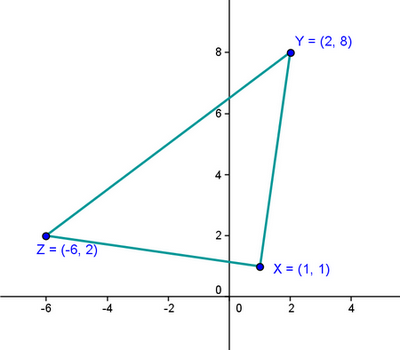
16.1


Dvě strany jsou stejně dlouhé, třetí strana evidentně delší tj.
ANO16.2

Skalární součin =0 tj. trojúhleník je pravoúhlý -
NE (Ostroúhlý troj. má všechny 3 úhly menší jak 90 stupňů)
16.3
Protože je trojúhelník rovnoramenný potom výška půlí stranu -
ANO16.4
Protože je troj. pravoúhlý potom výška je zároveň stranou -
NEPříklad 17)Trojúhelník ABC je určen délkami stran a=9 cm, b=15 cm, c=10 cm.
Jakou hodnotu (s přesností na setiny) má kosinus největšího úhlu?
A) +0,49
B) +0,12
C) -0,24
D) -0,49
E) -0,76
Největší úhel bude proti nejdelší straně.
Podle kosinové věty:

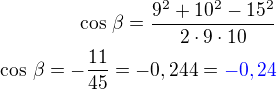
Tato odpověď je pod možností C)
Příklad 18)V oblasti se během dvou let počet obyvatel zvýšil z 24500 na 26500.
V obou letech byl zaznamenán stejný procentuální přírůstek oproti předcházejícímu roku
Jaký meziroční přírůstek byl zaznamenán?
A) méně než 4 %
B) přibližně o 4,0 %
C) přibližně o 4,1 %
D) přibližně o 4,2 %
E) více než 4,2 %
Platí: (geom.posloupnost)

Roční přírůstek:

procenta
V nabídce odpovědí je to možnost B) (přibližně o 4,0 %)
Příklad 19)Osm šéfů gangu představuje pouhá 2,5 % počtu všech členů gangu,
ale připadá na ně celá polovina zisku.
Kolikrát větší je průměrný zisk šéfa gangu oproti průměrnému zisku řadového člena?
A) 19 krát
B) 20 krát
C) 25 krát
D) 39 krát
E) 80 krát
Všech členů gangu je:

Řadových členů je:

Musí tedy platit: (zisk byl rozdělen na polovinu) tj. v poměru 1:1

krát větší zisk
V nabídce odpovědí je to možnost D)
Příklad 20)Průměrný plat 10 pracovníků byl 26800 Kč. Čtyřem pracovníkům zvýšlili plat o stejnou částku.
Proto se průměrný plat desetičlenné skupiny zvedl o 240 Kč.
O kolik korun si polepšil každý z platově zvýhodněných pracovníků ?
A) o 240 Kč
B) o 400 Kč
C) o 480 Kč
D) o 960 Kč
E) o jinou částku
Celkové zvýšení je o

Pro každého ze 4 pracovníků zvýšení činí

Kč
Z nabízených odpovědí je to možnost E) (o jinou částku)
Příklad 21)Tenisové míčky jsou natěsno baleny v plechovkách ve tvaru válce
Prodávají se po dvou, třech nebo čtyrech kusech.
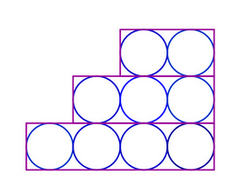
Ve které plechovce vyplňují míčky 2/3 jejího objemu?
A) libovolné
B) pouze v plechovce se 2 míčky
C) pouze v plechovce se 3 míčky
D) pouze v plechovce se 4 míčky
E) v žádné plechovce
Poměr objemů bude stejný ať už bude v plechovce 1 nebo 4 míčky
Pro 1 míček je poměr objemů míčku k celé plechovce:
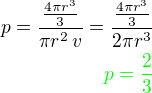
Poměr tedy platí pro libovolný počet míčků v plechovce
Odpověď A)Příklad 22)Je dána rovnice s neznámou


Ve kterém intervalu naleznete oba kořeny rovnice ?
A) <2; 6>
B) <0; 5>
C) <-4; 3>
D) <-6; -3>
E) v žádném z uvedených
Řešení výše uvedené rovnice je
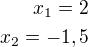 Kořeny jsou v intervalu pod bodem C)Příklad 23)
Kořeny jsou v intervalu pod bodem C)Příklad 23)Je dána rovnice s neznámou

 Řešením rovnice je:
Řešením rovnice je:A) prázdná množina
B) {0}
C) {0,1; 10}
D) (0; + nekonečno)
E) R\{0}
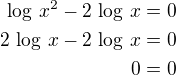
Řešením jsou všechna x z definičního oboru.
Logaritmus je definován pro kladná čísla tj definiční obor je interval
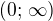
Správná odpověď se skrývá pod písmenem D)
Příklad 24)
Který ze zobrazených vektorů má souřadnice

?
A) a
B) b
C) c
D) d
E žádný
Vektor

je tvořen body:

a

vektor
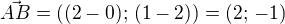
-
což je hledaný vektorOdpověď A)Příklad 25)Přiřaďte ke každému předpisu funkce f_1 - f_4 odpovídající název grafu (A-F)
A) přímka
B) parabola
C) hyperbola
D) kružnice
E) graf exponenciální funkce
F) jiný název
25.1
 - parabola (B)
- parabola (B)25.2
 - exponenciála (E)
- exponenciála (E)25.3
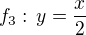 - přímka (A)
- přímka (A)25.4
 - hyperbola (C)
- hyperbola (C) Příklad 26)
Příklad 26)Přiřaďte výrazům (26.1 - 26.3) jejich ekvivalentní vyjádření (A-D)
26.1

-
Odpověď C)26,2

-
Odpověď D)26.3

-
Odpověď B)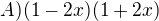
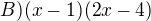







 a čitatel druhého zlomku násobíš
a čitatel druhého zlomku násobíš 

 a dostaneš tak zlomek:
a dostaneš tak zlomek:
 jde zkrátit a tak výsledný tvar bude:
jde zkrátit a tak výsledný tvar bude: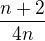

 upravte:
upravte:
 řešte:
řešte:

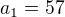

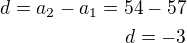



 kde
kde  , prochází bodem
, prochází bodem 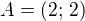

 a souřadnici y bodu
a souřadnici y bodu 
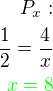
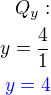




 tedy hledaný úhel bude:
tedy hledaný úhel bude: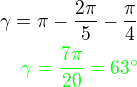

 a je kolmá k přímce q
a je kolmá k přímce q bude mít tvar:
bude mít tvar: dosazením souřadnic bodu A do předpisu dopočteme c
dosazením souřadnic bodu A do předpisu dopočteme c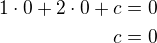

 procent
procent



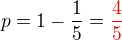
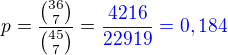


 cm^3
cm^3

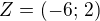





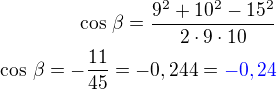

 procenta
procenta

 krát větší zisk
krát větší zisk
 Kč
Kč
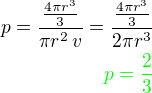


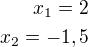

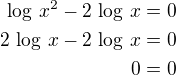
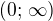

 ?
? je tvořen body:
je tvořen body:  a
a 
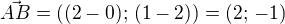 - což je hledaný vektor
- což je hledaný vektor

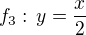


 -
-  -
-  -
-