Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Pekná úloha z teórie čísel 2 (ťažšia ako predošlá) (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 08. 2012 00:55 — Editoval BakyX (02. 08. 2012 00:55)
Pekná úloha z teórie čísel 2 (ťažšia ako predošlá)
Dobrý deň. Skúste si ďalšiu peknú úlohu z teórie čísel. Očakávam väčšiu odozvu, úloha mi príde zaujímavejšia ako predošlá, aj keď je trocha náročnejšia. Nebojte sa poslať aspoň jednu implikáciu.
Dokážte, že číslo 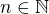 vieme napísať ako súčet aspoň dvoch po sebe idúcich prirodzených čísel práve vtedy, keď
vieme napísať ako súčet aspoň dvoch po sebe idúcich prirodzených čísel práve vtedy, keď  nie je v tvare
nie je v tvare 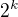 pre
pre 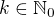 .
.
1^6 - 2^6 + 3^6 = 666
Offline
- (téma jako vyřešené označil(a) BakyX)
#2 02. 08. 2012 10:32 — Editoval OiBobik (02. 08. 2012 13:23)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Pekná úloha z teórie čísel 2 (ťažšia ako predošlá)
↑ BakyX:
Ahoj,
pěkná úloha. ; ))
Teď sem dám aspoň tu lehkou implikaci. Později se zamyslím nad tou druhou.
Z druhé přidám ještě lichá čísla, která jsou dost triviální:
No a tak ještě ta sudá:
Řešils to taky nějak takto, nebo nějak úplně jinak?
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 02. 08. 2012 20:39 — Editoval BakyX (02. 08. 2012 20:42)
Re: Pekná úloha z teórie čísel 2 (ťažšia ako predošlá)
↑ OiBobik:
Ahoj.
Ľahšia implikácia:
Ťažšiu implikáciu - pre nepárne
 mám rovnako, tam nie je čo riešiť.
mám rovnako, tam nie je čo riešiť. A čo sa týka ťažšej implikácie pre párne
 :
:Moje riešenia ťažšej implikácie pre párne
 :
: Prvé riešenie:
Druhé riešenie:
1^6 - 2^6 + 3^6 = 666
Offline
#4 02. 08. 2012 21:10 — Editoval OiBobik (02. 08. 2012 21:12)
#5 02. 08. 2012 23:24
- check_drummer

- Příspěvky: 4628
- Reputace: 99
Re: Pekná úloha z teórie čísel 2 (ťažšia ako predošlá)
↑ OiBobik:
Ahoj, kde jsi prosím využil v případě sudého n, že p je prvočíslo? Děkuji.
"Máte úhel beta." "No to nemám."
Offline
#6 02. 08. 2012 23:54 — Editoval OiBobik (03. 08. 2012 07:51)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Pekná úloha z teórie čísel 2 (ťažšia ako predošlá)
↑ check_drummer:
Ahoj,
to je pravda, vlastně nikde : )) stejně tak bych místo toho lichého prvočísla mohl uvažovat libovolného lichého dělitele většího než 1 (což má každé číslo, které není tvaru 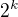 - a žádné z čísel v tomto tvaru takového dělitele nemá).
- a žádné z čísel v tomto tvaru takového dělitele nemá).
Důležitá tam byla ta lichost - kdybych to samý zkoušel se sudým dělitelem, uprostřed mi vyjde "schodek" o 2 (tj: prostřední dva sčítance takto vytvořené by se lišily o 2 (nebo o 0) ).
Ale tak napadlo mě to zkrátka s prvočíslem (žejo, když má člověk zadané nějaké kritérium typu "není tvaru 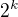 ", první věc, co ho napadne, je zkoumat prvočíselné rozklady).
", první věc, co ho napadne, je zkoumat prvočíselné rozklady).
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Pekná úloha z teórie čísel 2 (ťažšia ako predošlá) (TOTO TÉMA JE VYŘEŠENÉ)
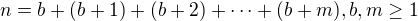 .
.  .
.  .
. sudé: Pak čísla
sudé: Pak čísla  jsou celočíselní dělitelé čísla
jsou celočíselní dělitelé čísla 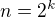 , tedy speciálně také tvaru
, tedy speciálně také tvaru  pro vhodná
pro vhodná  . Přitom
. Přitom 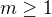 , tedy
, tedy 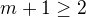 a je to liché číslo - to je spor.
a je to liché číslo - to je spor. přičemž čísla
přičemž čísla  jsou celočíselní dělitelé čísla
jsou celočíselní dělitelé čísla  a je to liché číslo - opět spor.
a je to liché číslo - opět spor. .
.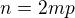 , kde
, kde  je liché prvočíslo. Lze psát
je liché prvočíslo. Lze psát 
 .
.  a je potřeba jen ošetřit, že nakonec nám zbudou alespoň dva sčítance. Kdyby ne, pak to znamená, že
a je potřeba jen ošetřit, že nakonec nám zbudou alespoň dva sčítance. Kdyby ne, pak to znamená, že  (tj. poslední člen toho rozvoje na sčítance je právě to celé číslo). Úpravou pak dostaneme
(tj. poslední člen toho rozvoje na sčítance je právě to celé číslo). Úpravou pak dostaneme  . Jelikož
. Jelikož 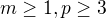 , dostáváme spor.
, dostáváme spor.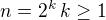 . Potom
. Potom 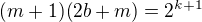 . Obe čísla
. Obe čísla  ,
, 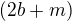 musia byť párne, avšak ich súčet je
musia byť párne, avšak ich súčet je 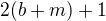 , čo je číslo nepárne, spor.
, čo je číslo nepárne, spor. napísať ako
napísať ako 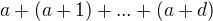 pre vhodné
pre vhodné 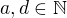 . Tento súčet vieme vyjadriť ako
. Tento súčet vieme vyjadriť ako  .
. 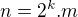 , kde
, kde 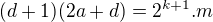 . Predpokladajme, že sme
. Predpokladajme, že sme  vhodne rozložili na súčin
vhodne rozložili na súčin  a že platí
a že platí  ,
,  . Ľahko vyjadríme
. Ľahko vyjadríme 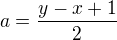 ,
,  . Postačujúca podmienka nato, aby
. Postačujúca podmienka nato, aby  existovali je zrejme to, že
existovali je zrejme to, že 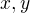 majú rôznu paritu a
majú rôznu paritu a  . Preto voľme
. Preto voľme 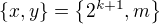 v takom poradí, že
v takom poradí, že  vznikne tak, že od súčtu
vznikne tak, že od súčtu  odrátame súčet
odrátame súčet 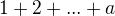 . Preto dokazujeme, že každé číslo
. Preto dokazujeme, že každé číslo 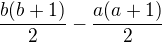 , kde
, kde  a
a  .
.  , čo môžme upraviť na
, čo môžme upraviť na 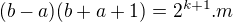 . Predpokladajme, že sme
. Predpokladajme, že sme  a
a  . Ľahko vyjadríme
. Ľahko vyjadríme  ,
, 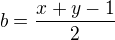 . Postačujúca podmienka na to, aby
. Postačujúca podmienka na to, aby 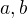 existovali je, že
existovali je, že  . Voľme preto
. Voľme preto