Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 08. 08. 2012 12:10 — Editoval Tychi (08. 08. 2012 12:15)
Re: Konstrukce trojúhelníku
↑ Oxyd: D je evidentně průsečík osy úhlu ACB se stranou AB..
↑ Keeeeke:Řekla bych, že ano, jen musím chvíli přemýšlet, jak tam nacpat nějaké otočení nebo tak něco.
Vesmír má čas.
Offline
#4 08. 08. 2012 14:01
Re: Konstrukce trojúhelníku
Ahoj ↑ Keeeeke:,
Skus pouzit znamu vlasnost osy u vrcholu C v Trojuholniku ABC
Poznamka:  je dlzka usecky
je dlzka usecky ![kopírovat do textarea $[AB]$](/mathtex/60/60306461b1981e5ae7a2b38767793e3c.gif)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 09. 08. 2012 16:31
Re: Konstrukce trojúhelníku
Offline
#6 09. 08. 2012 17:36
Re: Konstrukce trojúhelníku
Ano, kolega ↑ Rumburak:, ti dava vybornu radu.
(inac ta vlasnost o ktorej pisem sa da pouzit aj inac, napriklad Thalas-ova veta)
Ina cesta k rieseniu, je urcit geometricke miesto bodov M takych ze pomer  je dana konstanta.
je dana konstanta.
Navod
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 10. 08. 2012 18:45
Re: Konstrukce trojúhelníku
↑ Rumburak:↑ vanok:
Bezva kluci, diky. Nenapadlo Vas však, jak ho sestrojit bez počítání dalších stran? Díky
Offline
#8 11. 08. 2012 12:30
Re: Konstrukce trojúhelníku
↑ Keeeeke:,
V metode co som ti navrhol ↑ vanok:, netreba pocitat ziadne strany, treba len, urobit naznacenu konstukciu.
Skus ju presne popisat. ( a urobit aj na papiery)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 13. 08. 2012 12:23
Re: Konstrukce trojúhelníku
Offline
#10 13. 08. 2012 12:42
Re: Konstrukce trojúhelníku
Pozdravujem ↑ Honzc:,
Pekna didakticka konstrucia.
Pozri aj tu: http://fr.wikipedia.org/wiki/Cercles_d'Apollonius
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 14. 08. 2012 10:04
Re: Konstrukce trojúhelníku
↑ Keeeeke:
Připomenu jen, že algebraických vztahů mezi úsečkami v obrazci lze využít nejen k numerickým výpočtům, ale i k nalezení konstrukčních postupů.
Pomocí návrhů v příspěvcích ↑ vanok: a ↑ Rumburak: mi vyšlo
 ,
,
kde úsečky (či jejich délky)  jsou dány ať již numericky, nebo "graficky".
jsou dány ať již numericky, nebo "graficky".
Úsečku délky  pak sestrojíme z úseček o délkách
pak sestrojíme z úseček o délkách  metodou čtvrté geometrické úměrné, úsečku délky
metodou čtvrté geometrické úměrné, úsečku délky 
asi nejnázorněji sestrojíme pomocí Eukleidovy věty o odvěsně.
Offline


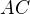 ,
, 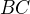 druhou rovnici .
druhou rovnici .