Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Listopadová nerovnost s odmocninou
#1 20. 11. 2008 12:28 — Editoval Marian (20. 11. 2008 13:47)
Listopadová nerovnost s odmocninou
Pro ty uživatele tohoto fóra, kteří sem nechodí jen demonstrovat řešení klasických úloh typu vypočtěte integrál nebo derivujte funkci bych tady měl jednu podzimní nerovnost. Za jednu z těch hezčích nerovností považuji tuto
Nechť  jsou kladná reálná čísla. Dokažte (samozřejmě mě zajímá co nejelementárnější důkaz) platnost nerovnosti
jsou kladná reálná čísla. Dokažte (samozřejmě mě zajímá co nejelementárnější důkaz) platnost nerovnosti
___________
Edit.: Pokud někomu překáží zápis se sumami, zpřístupnil bych to tímto přepisem:
Offline
- (téma jako nevyřešené označil(a) BrozekP)
#2 20. 11. 2008 21:15
Re: Listopadová nerovnost s odmocninou
↑ Marian:
Ahoj Marian,
všimol som si, že na fórum pridávaš mnoho zaujímavých príkladov na dôkazy. Všetky do jedného sú však pre mňa nezvládnuteľné. Mohol by si raz za čas pridať nejaké zadanie aj pre menej zdatnejších. Nepochybujem o kvalitách približne piatich výnimočných, ktorí sem prispievajú (vrátane teba :-), ale podľa mňa by bolo lepšie trošku úroveň náročnosti niektorých zadaní znížiť, aby sa mohli zapájať aj ostatní. Ja sem nechodím demonštrovať svoje "nabifľované" vzorce pre mladších kolegov, rád by som sa zapojil do riešenia tvojich úlohy, bohužiaľ zatiaľ márne. Je to určite prospešné, no tvoje úlohy rieši len hŕstka vyvolených, ktorým to skutočne ide od ruky :-) Pozdravujem vás. Nechcem tým však povedať, že napríklad tento dôkaz je ťažký, tak ho zmaž, ale len z času na čas sem hoď aj taký menej náročný, napríklad "Důkaz pro méne zdatné matematiky na podzim" :-))) Čo ty na to?
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 20. 11. 2008 21:36
Re: Listopadová nerovnost s odmocninou
↑ Marian:
Ahoj Mariane, uz dlouho se chystam k tomu, ze se pustim do nektere z tvych vyzev, zatim jsem ale nenasel dostatek casu. Timto bych si ale dovolil te poprosit, zda bys nepopatril na nedavno nove zavedene kategorie prave pro takovyto druh zajimavych prikladu a propriste umistoval svoj priklady tam. Prispeje to k prehlednosti a to predevsim pro takove, kteri tady na foru hledaji podobe zajimave ulohy.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#4 20. 11. 2008 22:13 — Editoval Marian (20. 11. 2008 22:14)
Re: Listopadová nerovnost s odmocninou
↑ lukaszh:
Uvědomil jsem si až teď, že rozškatulkovat účastníky fóra na ty, kteří pouze řeší některé úlohy a jiní se vrtají v každé drobnosti, není správné. Měl jsem to napsat výstižněji - omluva je asi na místě. Pokusím se dávat i jednodušší úlohy. Tahle se mi zdála velmi jednoduchá, až jsem našel chybu, takže, zatím nemám uspokojivé elementární řešení. A právě proto, abych nezapomínal i na kolegy, kteří se do matematiky teprve hlouběji dostávají, tak chci - s pomocí ostatních - najít elementární řešení, aby byl takovýto důkaz přístupný i jim. Beru na vědomí tvé připomínky a vezmu si z nich ponaučení.
↑ Lishaak:
Často tápu, co se myslí pod pojmem zajímavá úloha. Je to relativní pojem a já marně hledám nějaké vodítko k tomu, abych mohl o některé úloze rozhodnout a třeba vyřknout: "Tato úloha je zajímavá!". Příště se pokusím tyto věci umístit jinam.
Offline
#5 20. 11. 2008 22:48
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Listopadová nerovnost s odmocninou
Souhlasím, že by se pro to měla založit sekce. Přeci jen jde o příklady, kde zadávající často zná výsledek, jen ho zajímá řešení ostatních.
Jinak se mi zdá, že tyto příklady si dávají mezi sebou Marian, Pavel a BrozekP :)
Offline
#6 20. 11. 2008 23:52
Re: Listopadová nerovnost s odmocninou
↑ Marian:
Pokus o definici zajimave ulohy:
Ulohu nazveme zajimavou, pokud jeji autor prepoklada, ze jeji resitel ji bude resit pro poteseni ze samotneho procesu reseni, spise nez pro poteseni z toho, ze nekomu ulehcil zivot tim, ze mu sdelil vysledek.
Tedy "obycejne uloha" je zadosti o pomoc, naopak "zajimava uloha" je jakousi vyzvou ostatnim lidem aby predvedli, co vsechno umi.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#7 21. 11. 2008 09:42 — Editoval Pavel (21. 11. 2008 15:36)
Re: Listopadová nerovnost s odmocninou
↑ Marian:
Zatím se mi nerovnost dokázat nepodařilo. Dostal jsem se však velice blízko. Uvedu proto svou myšlenku, možná že se na tom dá stavět.
Použil jsem matematickou indukci:
Pro k=1 určitě platí 
nerovnost platí pro k=n-1. Pak
Výraz  je možné odhadnout na základě nerovnosti mezi aritmetickým (A), geometrickým (G) a harmonickým (H) průměrem. Použiju A-G nerovnost:
je možné odhadnout na základě nerovnosti mezi aritmetickým (A), geometrickým (G) a harmonickým (H) průměrem. Použiju A-G nerovnost:
Nyní použiju A-H nerovnost:
Pokud dám dohoromady nerovnosti, které jsem získal z A-G a z A-H, dostanu
Takže jsem dokázal, že
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 21. 11. 2008 14:29
Re: Listopadová nerovnost s odmocninou
↑ Pavel: Do toho geometrickeho prumeru by melo jit nasobeni a ne scitani... Take jsem sel touto cestou, ale zatim nedotahl. Jeste jsem si uvedomil, ze prava strana je symetricka, zatimco leva ne, a ze leva bude maximalni pro  . BÚJO tedy muzeme tohle uvazovat. Treba to pujde nejak vyuzit...
. BÚJO tedy muzeme tohle uvazovat. Treba to pujde nejak vyuzit...
Offline
#10 22. 11. 2008 16:08 — Editoval BrozekP (22. 11. 2008 16:10)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Listopadová nerovnost s odmocninou
↑ Pavel:
Udělal jsi určitě pěkný kus práce, ale dá se to nějak využít, když neplatí
(To je vidět např. pro  .)
.)
↑ lukaszh:
Myslím, že důkaz zde by mohl být zvládnutelný (jde o důkaz konečnosti algoritmu).
Offline
#11 22. 11. 2008 17:05
Re: Listopadová nerovnost s odmocninou
↑ Pavel:
Postupoval jsem jinak a dostal tuto nerovnost ...
Indukcí předpokládám, že platí pro fixní n nerovnost
Definuji čísla  jako
jako
kde čísla  jsou kladná čísla napřed daná. Dosazuji-li tato y_i za x_i do indukčního předpokladu, bude platit
jsou kladná čísla napřed daná. Dosazuji-li tato y_i za x_i do indukčního předpokladu, bude platit
Bohužel ani použitím tohoto triku nelze obecně ukázat, že platí
Toto zredukujeme na nerovnost
která ovšem obecně neplatí, což se snadno ukáže třeba tak, že nahradíme 
Offline
#12 22. 11. 2008 17:22
Re: Listopadová nerovnost s odmocninou
↑ BrozekP:
Děkuji za napomenutí. Příspěvek nedával žádnou novou informaci protože jsi přede mnou (aniž bych to postřehl) našel protipříklad. Smažu brzo i tento.
Offline
#13 22. 11. 2008 17:30 — Editoval BrozekP (22. 11. 2008 17:35)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Listopadová nerovnost s odmocninou
↑ Marian:
Já myslím, že pokud by byl správně bez té chyby, na kterou jsem upozornil, pak by novou informaci dával. Já jsem pouze ukázal, že odhad, který byl důsledkem všech úprav, které Pavel provedl, nestačil, ty by jsi ukázal, že už odhad v prvním kroku je nedostatečný.
Edit: Máš pravdu, můj protipříklad se dá použít už na první krok, nevšiml jsem si toho :-)
Offline
#14 22. 11. 2008 17:36
Re: Listopadová nerovnost s odmocninou
↑ BrozekP:
Máš pravdu, jen si myslím, že to je dobře vidět. Zkusil jsem proto jiný trik (viz ↑ Marian:), ale ani toto nestačí.
Offline
#15 23. 11. 2008 13:26 — Editoval Pavel (23. 11. 2008 14:32)
Re: Listopadová nerovnost s odmocninou
↑ BrozekP:
Máš pravdu, že moje úpravy na nerovnost nestačí. Chtěl jsem naznačit myšlenky a postupy, které by se snad při řešení mohly hodit. I chybná a nedostatečná řešení jsou k něčemu dobrá :-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#16 23. 11. 2008 13:34
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Listopadová nerovnost s odmocninou
Dá se snadno ukázat, že platí .
.
Tak mě napadlo, jestli by nebylo možné najít podobný vztah i pro n>1, který by bylo lehčí dokázat a jehož důsledkem by byl vztah, který se snažíme dokázat. Sám jsem ale nic takového pro n>1 nenašel.
Offline
#18 27. 11. 2008 09:39 — Editoval musixx (27. 11. 2008 11:03)
Re: Listopadová nerovnost s odmocninou
Nechme bokem pripad, ze vsechna 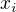 jsou jednicky.
jsou jednicky.
Plati  a rovnost je prave pro
a rovnost je prave pro 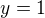 . Mohu tedy nejprve priostrit na
. Mohu tedy nejprve priostrit na .
.
To mohu upravit na .
.
Nyni mam vlevo pod odmocninama harmonicke prumery cisel  az
az  , tedy pod kazdou odmocninou to nemuzu zmensit, kdyz prejdu k prumerum aritmetickym, tedy celou nerovnost mohu priostrit na
, tedy pod kazdou odmocninou to nemuzu zmensit, kdyz prejdu k prumerum aritmetickym, tedy celou nerovnost mohu priostrit na .
.
Ted pro prehlednost vezneme  .
.
Zbyva ukazat pro kladna
pro kladna  , aspon jedno ruzne od 1, kde navic ve svetle meho predchoziho prispevku lze predpokladat, ze
, aspon jedno ruzne od 1, kde navic ve svetle meho predchoziho prispevku lze predpokladat, ze  (tezko ted rict, jestli to budeme k necemu potrebovat). Tato nerovnost mi prijde takova "ucesanejsi", a proto mozna snazsi k dokazani. Udelal jsem si nekolik prikladu (hrubou silou na pocitaci) a zda se, ze by tohle priostreni puvodni nerovnosti platit melo.
(tezko ted rict, jestli to budeme k necemu potrebovat). Tato nerovnost mi prijde takova "ucesanejsi", a proto mozna snazsi k dokazani. Udelal jsem si nekolik prikladu (hrubou silou na pocitaci) a zda se, ze by tohle priostreni puvodni nerovnosti platit melo.
EDIT:  nerostou, tedy mam pocit, ze nejhorsi pripad (tj. nejostrejsi nerovnost) nastane pro pripad, ze vsechny
nerostou, tedy mam pocit, ze nejhorsi pripad (tj. nejostrejsi nerovnost) nastane pro pripad, ze vsechny  jsou stejne. Je to ale jen muj "pocit": muzete mi tohle nekdo potvrdit/vyvratit? Pokud by to totiz byla pravda, pak je zbytek uz jen jednoducha indukce: Kdyz posledni nerovnost vydelim prave tim
jsou stejne. Je to ale jen muj "pocit": muzete mi tohle nekdo potvrdit/vyvratit? Pokud by to totiz byla pravda, pak je zbytek uz jen jednoducha indukce: Kdyz posledni nerovnost vydelim prave tim  , dostanu indukcni krok
, dostanu indukcni krok  , coz je pravda, nebot
, coz je pravda, nebot  (staci si to secist a umocnit).
(staci si to secist a umocnit).
Offline
#19 27. 11. 2008 16:07 — Editoval BrozekP (27. 11. 2008 20:42)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Listopadová nerovnost s odmocninou
↑ musixx:
Obávám se, že to už neplatí. Pošleme  do nekonečna a tedy
do nekonečna a tedy  do nuly. Měli bychom tak dostat
do nuly. Měli bychom tak dostat
ale to pro dostatečně velká n (stačí n=4) neplatí.
Offline
#20 04. 12. 2008 12:55 — Editoval Marian (04. 12. 2008 12:58)
Re: Listopadová nerovnost s odmocninou
S odstupem času jsem se díval na důkaz této nerovnosti a trochu jsem pokročil. Rád bych upozornil přinejmenším na to, že nerovnost lze ekvivalentně zaspat v jiném (podle mě pohodlnějším) tvaru.
Definujeme-li totiž
pak původní nerovnost přejde na tvar
Je samozřejmě splněno  . Podařilo se mi dokázat, že bude-li platit pro libovolné tři po sobě jdoucí prvky
. Podařilo se mi dokázat, že bude-li platit pro libovolné tři po sobě jdoucí prvky  podmínky
podmínky
pak nerovnost platí.
Možná, že ten přepsaný tvar bude někomu říkat více než mě.
Offline
#21 28. 01. 2009 17:31 — Editoval BrozekP (28. 01. 2009 17:31)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Listopadová nerovnost s odmocninou
Bohužel, svůj souboj s limitou vzdávám. Zkoušel jsem všechno možné co mě napadlo. Jen uvedu pár výsledků, které by snad někomu mohly pomoct při řešení nebo ho alespoň ušetřit od slepých uliček.
1.
(protipříkladem je např.  ,
,  )
)
2.
Neexistuje taková funkce  , že by pro všechna
, že by pro všechna  platilo
platilo .
.
Teď i nějaký pozitivní výsledek:
3.
Označím  a
a .
.
Dokazujeme tedy kladnost všech funkcí 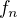 . Zřejmě
. Zřejmě 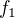 je kladná. Jestliže budeme dokazovat indukcí, můžeme předpokládat, že
je kladná. Jestliže budeme dokazovat indukcí, můžeme předpokládat, že  je kladná a z toho dokazovat, že je kladná i
je kladná a z toho dokazovat, že je kladná i 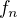 . Platí
. Platí .
.
Pokud nemá 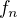 jako funkce
jako funkce  minimum, pak je zřejmě klesající a kladná. Pokud má minimum, pak v něm derivace musí být nulová.
minimum, pak je zřejmě klesající a kladná. Pokud má minimum, pak v něm derivace musí být nulová.
Aby byla derivace nulová, musí platit .
.
Stačí tedy dokázat, že je 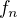 kladná (tj. platí dokazovaná nerovnost) v bodě s n-tou souřadnicí
kladná (tj. platí dokazovaná nerovnost) v bodě s n-tou souřadnicí  takovou, že je splněno
takovou, že je splněno .
.
Doufám, že to někomu pomůže :-)
Edit: A už nejsem Einstein :-(
Offline
#22 28. 01. 2009 18:37 — Editoval Marian (28. 01. 2009 18:37)
Re: Listopadová nerovnost s odmocninou
↑ BrozekP:
Obdivuji tvůj elán a nasazení. A samozřejmě také zájem řešit tuto úlohu. Pokusím se atakovat řešení zase někdy později. Někdy tak vyplynou některé nové skutečnosti. Možná to chce ještě jinou strategii (třeba nějaká méně zřejmá transformace nerovnosti). Věřím, že se o řešení pokusí i ostatní.
Offline
#23 04. 02. 2009 07:59 — Editoval musixx (04. 02. 2009 08:54)
Re: Listopadová nerovnost s odmocninou
Rozdelme cely dukaz na tri kroky. Dokazujeme, ze pro kladna realna cisla plati nerovnost
Pro prehlednost nebudu psat sumy, ale tri tecky.
Krok 1: Ukazu, ze pozadovana nerovnost plati, jsou-li vsechna 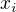 nejvyse jednicky.
nejvyse jednicky.
Pak je totiz vlevo nanejvys  a vpravo je alespon
a vpravo je alespon  . Dokazme tedy indukci silnejsi tvrzeni, a to ze
. Dokazme tedy indukci silnejsi tvrzeni, a to ze .
.
Zrejme pro 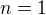 je
je  . Podle indukcniho predpokladu je
. Podle indukcniho predpokladu je  , staci tedy ukazat, ze
, staci tedy ukazat, ze  , neboli
, neboli  . Zde jde o nerovnost mezi nezapornymi cisly, tedy umocneni je ekvivalentni uprava a staci dokazat, ze
. Zde jde o nerovnost mezi nezapornymi cisly, tedy umocneni je ekvivalentni uprava a staci dokazat, ze  , neboli ze
, neboli ze  . Opet jde o nerovnost mezi nezapornymi cisly, tedy staci ukazat, ze
. Opet jde o nerovnost mezi nezapornymi cisly, tedy staci ukazat, ze  , tedy ze
, tedy ze  . Ukazu dokonce vic, a to ze citatel zmenseny o 1 a vydeleny
. Ukazu dokonce vic, a to ze citatel zmenseny o 1 a vydeleny 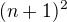 je kladny. Je totiz
je kladny. Je totiz  , coz je zrejme kladne.
, coz je zrejme kladne.
Krok 2: Ukazme, ze vyraz vpravo je maximalni pro  .
.
Kdyby totiz existovaly takove  , ze
, ze  , pak prinejmensim i-ty scitanec je mensi nez i-ty scitanec v pripade, ze vsechna
, pak prinejmensim i-ty scitanec je mensi nez i-ty scitanec v pripade, ze vsechna  jsou setrizena nevzestupne.
jsou setrizena nevzestupne.
Krok 3: Dokazme nerovnost v plne obecnosti. Podle jiz drive dokazanych dvou kroku mohu predpokladat, ze  .
.
Mohu psat



Nebot jsou 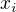 nerostouci, jsou cisla
nerostouci, jsou cisla  pro
pro  mensi nez 1, tedy podle jiz dokazaneho v kroku 1 mohu zatim napsane zvetsit na
mensi nez 1, tedy podle jiz dokazaneho v kroku 1 mohu zatim napsane zvetsit na . Protoze jsme ale v kroku 3 mohli bez ujmy na obecnosti predpokladat, ze
. Protoze jsme ale v kroku 3 mohli bez ujmy na obecnosti predpokladat, ze  , a dale protoze zrejme plati
, a dale protoze zrejme plati  , mohu vyraz dale zvetsit na
, mohu vyraz dale zvetsit na 
 .
.
Mame tedy ukazat, ze , neboli ze
, neboli ze .
.
Oznacme ted  . Zrejme je
. Zrejme je  nezaporne. Zbyva tedy ukazat, ze
nezaporne. Zbyva tedy ukazat, ze . Jde o nerovnost mezi nezapornymi cisly, tedy je ekvivalentni nerovnosti
. Jde o nerovnost mezi nezapornymi cisly, tedy je ekvivalentni nerovnosti , tedy
, tedy  , coz je opet nerovnost mezi nezapornymi cisly, tedy je ekvivalentni nerovnosti
, coz je opet nerovnost mezi nezapornymi cisly, tedy je ekvivalentni nerovnosti , tedy nerovnosti
, tedy nerovnosti  , ktera je pro nezaporne
, ktera je pro nezaporne  (coz vime) platna.
(coz vime) platna.
EDIT: Mam tam chybku, ale doufam, ze uz nejsme daleko od reseni. Kdyz uz jsem to vsechno napsal, tak to tu zverejnim. Treba ji odstrani nekdo driv nez se k tomu dostanu sam... Kdo ji chce identifikovat sam, at se nediva do skryteho textu.
EDIT2: Hrani si s touto nerovnosti me v jedne fazi privedlo na funkci
 definovanou jako
definovanou jako  . Zda se, ze tato funkce by mohla mit zajimavou limitu pro
. Zda se, ze tato funkce by mohla mit zajimavou limitu pro 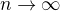 (chcete-li ji nejak rozsirit na realnou funkci, scitejte v sume treba do cele casti z n). Je totiz
(chcete-li ji nejak rozsirit na realnou funkci, scitejte v sume treba do cele casti z n). Je totiz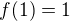





Chce se s tim nekomu trochu pohrat?
Offline
#24 04. 02. 2009 13:26
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Listopadová nerovnost s odmocninou
↑ musixx:
Já tam vidím chybu v začátku, levá strana je největší pro všechny 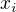 jdoucí do nuly, je tedy nejhůře n a pravá strana je nejméně
jdoucí do nuly, je tedy nejhůře n a pravá strana je nejméně  . To tedy nestačí, levá strana vždy přeroste pravou.
. To tedy nestačí, levá strana vždy přeroste pravou.
Krok 2 mi moc není jasný, asi tam máš překlepy (levá/pravá, i-tý/j-tý). Pravá strana je stejná ať už zvolíš libovolné pořadí, takže jsi asi chtěl mluvit o levé. Ta je ale největší pro  , jak už jsi psal dříve.
, jak už jsi psal dříve.
Jsou to ty chyby, které myslíš ty?
Offline
#25 04. 02. 2009 15:00
Re: Listopadová nerovnost s odmocninou
↑ musixx:
Výpočet tebou uvedené limity je zajímavá konstanta ...
Offline
Stránky: 1 2
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Listopadová nerovnost s odmocninou


 .
.