Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 08. 2012 23:12 — Editoval yaqwsx (14. 08. 2012 08:58)
Zrychlení při kruhovém pohybu
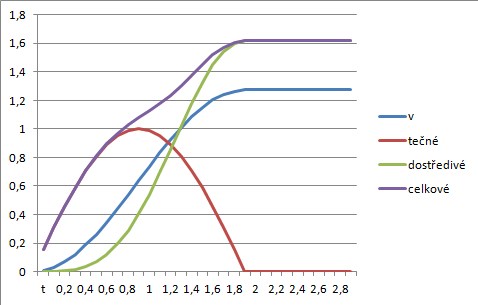
Snažím se matematicky popsat pohyb tělesa po kružnici, které se pohybuje s tečnovým zrychlením, které má sinový průběh. Tzn. úhlové zrychlení má následující průběh: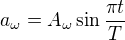
kde 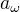 je úhlové zrychlení, t je čas, T je perioda průběhu a
je úhlové zrychlení, t je čas, T je perioda průběhu a  je maximální úhlové zrychlení.
je maximální úhlové zrychlení.
Zintegrováním dostanu vztah pro okamžitou úhlovou rychlost: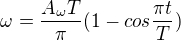
Celkové zrychlení, se kterým se těleso pohybuje spočítám pomocí Pythagorovy věty: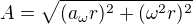
Když dosadím: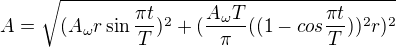
Vstupem do tohoto výpočtu je cílová rychlost  , které je nutno dosáhnout, maximální možná úhlová dráha
, které je nutno dosáhnout, maximální možná úhlová dráha  , na které je možné této rychlosti dosáhnout a maximální celkové zrychlení
, na které je možné této rychlosti dosáhnout a maximální celkové zrychlení  , které nesmí být překročeno. Pokud není možno dosáhnout
, které nesmí být překročeno. Pokud není možno dosáhnout  na dráze
na dráze  bez překročení
bez překročení  , potřebuji zjistit novou (nižší) rychlost
, potřebuji zjistit novou (nižší) rychlost  pro kterou to lze.
pro kterou to lze.
Zatímco u lineárního pohybu jsem řešení tohoto problému našel během chviličky, tady nevím. Pomalu si začínám myslet, že klasické řešení neexistuje - vidím zde mnoho cyklických závislostí.
Nemáte někdo nějaký nápad? Za jakékoliv nepřesnosti/opomenutí se omlouvám - hledím na to už pár dní a trochu mi začíná vynechávat hlava.
Offline
- (téma jako vyřešené označil(a) yaqwsx)
#2 15. 08. 2012 16:06
Re: Zrychlení při kruhovém pohybu
Je to hodně komplikované. Píšeš, co je "vstupem", ale není úplně jasné , co má být "výstupem" - snad vzorec pro časový průběh velikosti zrychlení,
jak by se zdálo z posledního uvedeného výpočtu ? Zkus co nejpřesněji zformulovat zadání.
Offline
#3 15. 08. 2012 20:16
Re: Zrychlení při kruhovém pohybu
Výstupem by měl být vzorec pro zjištění maximální hodnoty úhlové rychlosti a úhlového zrychlení, tak aby nikdy nebyla překročena velikost vektoru celkového zrychlení A a zároveň celý pohyb trval co nejkratší dobu (tzn. byl co nejdynamičtější).
Jak jsem na to chtěl jít - chtěl jsem si zderivováním posledního vzorce a následným porovnáním s nulou zjistit, kterém bodě nastává maximální hodnota zrychlení. Jelikož je to složitý vzorec, vložil jsem jej do Wolframu. Dostal jsem z něj však nesmysl - 6 řešení, z nichž 4 jsou komplexní řešení a zbývající 2 nedávají smysl; ve vzorci vycházel výraz 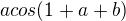 , kde
, kde  (a, b byly zlomky).
(a, b byly zlomky).
Když jsem si však celou situaci nakreslil do grafu a vyzkoušel celkem velký rozsah hodnot, dospěl jsem k závěru, že pro mě s dostatečnou přesností postačuje řešení, kdy maximální hodnoty zrychlení je dosaženo buď v čase  anebo
anebo 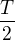 . A pokud se řešení nachází někde mezi těmito hodnotami, tak je to buď velice blízko jedné z nich anebo je průběh celkového zrychlení mezi nimi téměř konstantní.
. A pokud se řešení nachází někde mezi těmito hodnotami, tak je to buď velice blízko jedné z nich anebo je průběh celkového zrychlení mezi nimi téměř konstantní.
Ale i když jsem si zavedl toto zjednodušení a různě jsem podosazoval, tak jsem nedobral žádného řešení. Vždy mi z toho vyšla nějaká blbost.
Offline
#4 16. 08. 2012 10:16 — Editoval Rumburak (17. 08. 2012 10:23)
Re: Zrychlení při kruhovém pohybu
↑ yaqwsx:
Tomu zadání tedy rozumím tak, že máme dánu časovou závislost úhlového zrychlení, tj. konstanty  ve vzorci
ve vzorci
(1)  .
.
Jeho integrací dostaneme časovou závislost úhlové rychlosti
(2) 
a další integrací časovou závislost úhlové dráhy (či jak se to jmenuje)
(3)  ,
,
kde  jsou integrační konstanty, jeichž hodnoty volíme podle úhlové rychlosti a úhlové dráhy v okamžiku
jsou integrační konstanty, jeichž hodnoty volíme podle úhlové rychlosti a úhlové dráhy v okamžiku 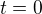 .
.
Volit 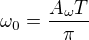 jistě není problém.
jistě není problém.
Extrémy úhlového zrychlení (1) nastávají v časových bodech  , kdy
, kdy  ,
,
obdobně extrémy úhlové rychlosti (2) nastávají v časových bodech  , kdy
, kdy 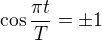 .
.
Zda bude nebo nebude překročeno "celkové zrychlení" (patrně velikost vektorového součtu tečného a normálového zrychlení při pohybu
bodu po kružnici) se musí ověřit, ale není mi jasné, k čemu je dobré tyto principiálně různé (i když příbuzné) fyzikální veličiny porovnávat.
Co myslíš tím, aby pohyb trval co nejkratší dobu ?
Popsaný pohyb, který je v jistém smyslu periodický, bude celkově trvat tak dlouho, dokud ho uměle nezastavíš :-).
EDIT. Závěrečnou úvahu z předchozí verze jsem smazal, protože byla nesprávná.
Offline
#5 16. 08. 2012 19:00
Re: Zrychlení při kruhovém pohybu
Díky za odpověď, ale asi jsem špatně popsal zadání. Zkusím to znovu a obsáhleji. Jak jsem v tom ponořený, asi už spoustu věcí beru za samozřejmost a opomínám je zmínit.
Celý tento výpočet dlouží jako model po kinematiku robotického ramene, které se pohybuje po zadané trajektorii popsané přímkami a kruhovými oblouky (do budoucna možná i složitějšími křivkami). Cílem je, aby se rameno mohlo pohybovat co nejrychleji, tzn. celou trajektorii projet co největší rychlostí. Tuto rychlost limituje mechanická konstrukce stroje. Po spoustě úvah, zkoušení a měření jsem dospěl k závěru, že téměř ideální pohyb je pokud má jeho zrychlení sinový průběh. Tehdy je průběh rychlosti plynulý a nevznikájí rázy a konstrukce je nejméně namáhana - tedy na své hranice se dostane při pohybu větší rychlostí. Na základě tohoto jsem implementoval pohyb pro přímce a sinusoidě (pro navázání jednolivých segmentů - získám plynulejší pohyb bez nutnosti brzdit za cenu malého zkraslení tvaru trajektorie). Výsledky byly nad očekávání dobré. Vzešlo z nich, že limit mechanické konstrukce charakterizuje max. velikost zrychlení  , která je tedy konstantou. (Doplním, že pro nízké rychlosti by bylo ještě vhodné zavést omezení maximálního ryvu
, která je tedy konstantou. (Doplním, že pro nízké rychlosti by bylo ještě vhodné zavést omezení maximálního ryvu  , ale to prozatím nechávám být a budu řešit v budoucnu).
, ale to prozatím nechávám být a budu řešit v budoucnu).
Nyní se snažím tento poznatek přenést i pro pohyb po kruhovém oblouku. Pokud se na oblouku pohybuji konstatní rychlostí, není problém určit mezní rychlos  , potažmo úhlovou rychlost
, potažmo úhlovou rychlost  , kdy není překročeno špičkové zrychlení
, kdy není překročeno špičkové zrychlení  . Problémem je, že na kružnici často potřebuji zrychlovat či zpomalovat.
. Problémem je, že na kružnici často potřebuji zrychlovat či zpomalovat.
Začal jsem tedy mou úvahu - odovodil jsem si sadu vzorečků pro lineární pohyb se sinovým zrychlením. (uvádím zde pouze případ zrychlování z nulové rychlosti na cílovou - pro zjednodušení). Zde jsou:
zrychlení lineárního pohybu má průběh: 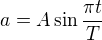
, kde konstantou stroje je pouze  , peridodu
, peridodu  spočítám z následujích vztahů (např. pokud chci maximální rychlost, či zadanou)
spočítám z následujích vztahů (např. pokud chci maximální rychlost, či zadanou)
rychlost lineárního pohybu má průběh: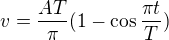
dráha lineárního pohybu (potažmo vzdálenost od počátku) má následující průběh:
Celkovou dráhu, kterou těleso urazí za periodu T zjistím následovně: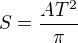
Ze vzorce pro rychlost, jsem schopen určit potřebnou délku periody, abych dosáhl zadané rychlosti (tedy  si volím, je vstupní proměnnou):
si volím, je vstupní proměnnou):
A maximální rychlost, kterou jsem schopen dosáhnout na zadané dráze zjistím následovně: 
, kde 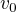 je počáteční rychlost na začátku úseku a
je počáteční rychlost na začátku úseku a  je brzdná (koncová rychlost) na konci úseku. Obě tyto rychlosti si volím (jsou vstupem)
je brzdná (koncová rychlost) na konci úseku. Obě tyto rychlosti si volím (jsou vstupem)
Protože se však pohybuji po kružnici, je pro mě výhodné uvažovat úhlovou rychlost - když tedy do výše uvedených vztahů dosadím místo rychlosti (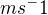 ) úhlovou rychlost(
) úhlovou rychlost( ), místo dráhy (
), místo dráhy ( ) úhlovou dráhu (úhel) (
) úhlovou dráhu (úhel) ( ) a místo zrychlení (
) a místo zrychlení (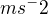 ) úhlové zrychlení (
) úhlové zrychlení (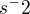 ), tak budou platit.
), tak budou platit.
Tím jsem měl vyřešen problém s kontrolou rychlosti. Nastava však otázka, jakou hodnotu má hodnota  . Logicky má takovou hodnotu, aby se výraz:
. Logicky má takovou hodnotu, aby se výraz:
ve svém maximu rovnal hodnotě maximálního zrychlení  . Potřebuji tedy zjistit, jakou maximální úhlovou rychlostí
. Potřebuji tedy zjistit, jakou maximální úhlovou rychlostí  a s jakým maximálním špičkovým úhlovým zrychlením
a s jakým maximálním špičkovým úhlovým zrychlením  se můžu pohybovat, abych nepřekročil maximální povolené zrychlení
se můžu pohybovat, abych nepřekročil maximální povolené zrychlení  . Tady se trochu poopravím - hodnotu T nepotřebuji zjistit - tu zjistím z výše uvedených veličin.
. Tady se trochu poopravím - hodnotu T nepotřebuji zjistit - tu zjistím z výše uvedených veličin.
Mám teď rozpracovaný další nápad, jak to spočítat, ale zatím ho sem nechci posílat - až jestli se mi bude zdát, že to není slepá ulička.
Offline
#6 17. 08. 2012 03:01 — Editoval rughar (17. 08. 2012 03:22)
Re: Zrychlení při kruhovém pohybu
Ahoj. Myslím že chápu co chceš. Původní vzoreček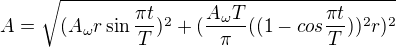
A snaha v něm hledat maximum je podle mě skutečně to, co hledáš. A souhlasím, nalézt t, pro které je zrychlení maximální, je dost nehezký výpočet. Vzoreček je sice dlouhý, ale ne neřešitelný. Mě wolfram krom t=0 (kde je evidentně minimum) a komplexích blábolů (tam se s časem opravdu nedostaneme) vyšla dvě řešení s opačnými znaménky. Můžeme bez problému uvažovat jen jedno z nich z odkazem, že se budeme věnovat pouze kladým časům. Takže zbývá pouze![kopírovat do textarea $t=\frac{T \text{ArcCos}\left[1+\frac{i \left(i+\sqrt{3}\right) \pi ^{8/3}}{2 6^{1/3} \left(9 A^4 T^8+\sqrt{-6 A^6 \pi ^4 T^{12}+81 A^8 T^{16}}\right)^{1/3}}-\frac{i \left(-i+\sqrt{3}\right) \pi ^{4/3} \left(9 A^4 T^8+\sqrt{-6 A^6 \pi ^4 T^{12}+81 A^8 T^{16}}\right)^{1/3}}{2 6^{2/3} A^2 T^4}\right]}{\pi }$](/mathtex/63/6389e9f36bc321f3ae8dc26c841d0308.gif) (*)
(*)
(z důvodu kopírování z wolframu u výrazu (*) je A označena veličina, která má být označena  )
)
Zde bych rád zdůraznil na zradu od Wolframu, které jsem si všimnul a je mimochodem možné, že tě stejně zradil i tvůj Wolfram. Při výběru "správného" reálného řešení není košer se ohlížet na to, který výraz obsahuje v sobě "íčko". Tento jako jediný (kromě triviálního t=0) je reálným, ačkoli "íčko" obsahuje a naopak jiné výstupy jej neobsahují. Výstupy wolframu se musí brát s rezervou, neboť na tvrdo uvádí výraz, kterému i když jasně řeknu, že A>0 a T>0, tak stejně si ve výrazu nechá podle těchto podmínek něco záporného pod odmocninou. Při zachování reálných A a T je skutečně výše zmíněný výraz reálný.
Pak je tady zrada od wolframu číslo dva. Ten výraz je skutečně reálný, ale pouze někdy. Pro dostatečně velké amplitudy zrychlení oproti periodě T výjdou komplexní úplně všechna řešení a zůstane pouze t=0. To naprosto sedí s tvými obrázky. V jednom případě je uprostřed intervalu někde maximum a v jednom případě vymizí a je na okraji.
A zrada wolframu číslo tři. Je naprosto evidentní, že pokud je maximum pro nějaký čas t, je určitě i pro nějaký čas t + 2T, někdy i v t + T. To ale wolfram nějak odignoruje a nechá jen to první. Krom řešení t=0 tedy je jistě řešením i t=T. A osobně z toho vidím vyvození následovné:
1) Pokud výraz (*) je reálný pro hodnota A,T, pak se zde nachází maximum pro zrychlení (a zároveň -- teď pozor -- ve všech bodech zvětšených o hodnotu 2T) a v bodech t = 0, t = T, t = 2T, t = 3T , ... má velikost zrychlení své minimum -- je zde nulové
2) Pokud výraz (*) je komplexní pro hodnoty A,T, pak jsou extrémy pouze v bodech t = 0, t = T, t = 2T, ... kde platí, že v .......... minimum
.......... minimum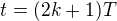 ......... maximum
......... maximum
Tohle celé k času t a tomu, že ti to nevyšlo. Nejspíš je chyba jen v interpretaci výstupu wolframu. Pozor na ta slavná "íčka".
Tedy sumasumarum. Mame t, kde je maximum. Dosazeni tohoto velkeho vyrazu do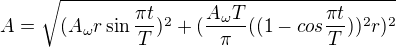
se dostane maximalni zrychleni. Maximalni rychlost jiz neni slozite najit.
To je z vyrazu 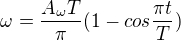
jasne videt, ze velikost maximalni uhlove ryhclosti je
(stačilo si uvědomit, kdy má cosinus nejvyšší hodnotu)
A drobna diskuse k závěru. To, zda-li t umístit na okraj nebo někam "doprostřed" dle výrazu (*) (toto rozhodnutí provádíme na základě toho, zda je vychází (*) komlplexní nebo reálné) se nejspíš ani u tebou reálně popisovaného experimentu nedá laxně přejít zanedbáním. Nahrazení (*) přibližnou hodnotou T/2 bude zřejmě při porovnání s experimentálními daty velmi dobře sedět. Vykreslim-li si prubeh t, kde dochazi k maximu zrychleni, v zavilsoti na konstantach Aomega, T tak dostanu takovy prubeh
obrazek v pdf
Na spodních osach ma interval 0..8 veličina A, a 0..2 patří veličině T (vše jednotky SI). To, co je pak v grafu vyneseno do horizontálního směru, je hodnota t/T , kde t je právě ten čas, kde je A maximílní. Je vidět, že tvůj odhad umístit ho zhruba do 0.5T je velmi dobrý. Je patrné, že tam vzniká jakási "hranice" ve tvaru skoro hyperboly. To je právě ta oblast, kde nám (*) skočí do imaginárních hodnot a maxima jsou pak na hranicích periody. Mimochodem. Na te "hranici" má na tom obrázku t/T hodnotu přesně 2/3. I když se to tváří na nějakých 0.58 - inu, numerické halo. To, že výraz (*) se nachází triktně v intrvalu T/2 .. 2T/3, tak je zcela analytický výsledek. Ale už ho nebudu rozpeisovat. Je to prostě jen gymnastika s wolframem. Kdybys o to stál, tak ti to klidně pošlu.
Na závěr ještě přidám jeden analytický výsledek. To, kdy je (*) komplexní a jdy ne. Tedy jaké podmínky mají platit pro Aomega a T, abychom použili buď (*) nebo umístili maximum do okraje. Dá se též odvodit, že (*) je potřeba použít právě tehdy, když
když je rovno, jsme na pomezí. A to je právě ten případ (a současně návod jak k tomu přijít), kde je t/T rovno 2/3.
----------------
jesště jsem si všimnul, že jsem dost vágně střílel, jak to bude s tím řešením, když jedno výjde v nějakém bodě t, tak další bude v bodě t + 2T. vidím žemi to někde nesedí, ale to nevadí. Pro účely příkladu stačí vskutku zkoumat pouze interval 0..T. A tedy mohou nastat pouze 2 možnosti
1)
(*) ...... maximum
t=0, t=T ...... minimum
2)
t=0 ...... minimum
t=T ...... maximum
----------------
a ještě než usnu :P, tak je vidět hezká analytická vlastnot, že výraz (*) lze přepsat do tvaru, že
, kde f je docela složitá funkce, ale v našem pojetí je to funkce jedné proměnné (a z intervalu 1/2...2/3, pokud je reálná). Tedy že t/T lze zapsat jako funkcí A_{\omega} T^2. Je možná komplikované, jak t závisí na A a T, ale co lze s jistotou tvrdit, že to vyjde stejně, pokud se zachová hodnota výrazu A_{\omega} T^2
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#7 17. 08. 2012 18:42
Re: Zrychlení při kruhovém pohybu
Díky za vyčerpávající odpověď. Při čtení tvé odpovědi jsem musel párkrát složit hlavu do rukou a říct si, jak blbej jsem, že jsem si toho nevšiml. Pravda, s Wolframem nedělám - jen občas k němu zabrousím.
Ačkoliv v Tvé odpovědi nebyl vyřčena přímo odpověď na mou otázku, pomohla mi si v hlavě udělat jasno a pořádek.
Držel jsem se mého posledního předpokladu - výsledek je buď T, T/2 anebo v těsné blízkosti za T/2. Dostal jsem 2 vzorečky; První pro případ, kdy maximum je v T: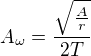
A druhý pro maximum v T/2, popř. v blízkosti za ním: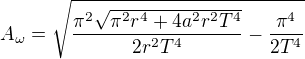
Napsal jsem si krátký program (simulaci), který na základě těhto vzorečků generuje rychlosti a nakrmil jsem ho reálnými daty a navíc jsem podle Tvého vzorečku určoval maximum. Tato data mě příjemně překvapila - nenastala jediná situace, kdy by maximum vyšlo "někde daleko mezi T/2 a T". Vždy jedno ze zrychlení zásadně převažovalo - tedy buď bylo "dominantní" tečné a nebo dostředivé. Rozdíl by relativně velký a tedy odchylka skutečného maxima od T/2 byla jen v řádu setin procenta - největší napočítaná odchylka byla 0,08% z T. Pro určování výsledné rychlosti naprosto dostačující a výrazně zjednodušující výpočet. A i kdyby v praxi nastala data, kdy by byla odchylka větší, tak ze zjednodušeného vzorce vyjde rychlost o něco měnší, něž je ta skutečná maximální - nikdy tedy nenastane situace, kdy by stroj pracoval nad maximální rychlostí.
Ještě jednou díky za odpověď - bez tohoto tématu bych se snad odpovědi nidky nedobral anebo by mi to trvalo mnohem déle.
Offline
#8 29. 03. 2013 16:10
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Zrychlení při kruhovém pohybu
Zdravím,
kolega se podělil o ukázku projektu, pěkné :-)
Offline