Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 08. 2012 16:48
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Inflace po 20 rokoch
http://www.realisticky.cz/ucebnice/01%2 … y%20II.pdf
Urči hodnotu 1 500 000 KČ po 20 rokoch, ak priemerna ročna inflacia bude  ? 6. uloha
? 6. uloha
Mne vychádza 915 406,40 KČ.
Prečo je tam - ?
Offline
- (téma jako vyřešené označil(a) miso16211)
#2 14. 08. 2012 17:48
Re: Inflace po 20 rokoch
↑ miso16211:
protože inflace peníze znehodnocuje.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 14. 08. 2012 18:24
Re: Inflace po 20 rokoch
↑ miso16211:
Podle knihy i podle meho vypoctu to vychazi jinak, jak jsi postupoval? Nebo se jedna o numerickou chybu?
„Jestliže neumíš – naučíme, jestliže nemůžeš – pomůžeme ti, jestliže nechceš – nepotřebujeme tě.“ —Jan Werich
Offline
#4 14. 08. 2012 18:27 — Editoval Pavel Brožek (19. 08. 2012 19:32)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Inflace po 20 rokoch
↑ miso16211:
Myslím, že jde o to, že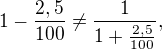
ale v tom materiálu to asi zaměňují. Přitom to platí pouze přibližně. Ale moc jsem to nezkoumal, možná to tam mají použité správně, vážně nevím…
Offline
#5 14. 08. 2012 19:34 — Editoval miso16211 (14. 08. 2012 19:36)
#6 16. 08. 2012 16:58 — Editoval peter_2+2 (18. 08. 2012 08:03)
Re: Inflace po 20 rokoch
↑ miso16211:
představ si množství něčeho v podobě úsečky -> úsečka "A"
A ____________________
zvětšíš úsečku např. o 10% -> vznikne množství B
B ____________________ __
Teď se znova podívej na ty dvě úsečky, jaký k sobě mají poměr
A ____________________
B ______________________
A : B je 100:110
A inflace např. oněch 10% ti říká, že zatímco HODNOTA PENĚZ v tom daném roce je "B" tak další rok bude "A" (na těch úsečkách sám vidíš, že klesá)
Čili 100/110 × HODNOTA PENĚZ nebo taky HODNOTA PENĚZ / (110/100)
110/100 se v desítkové soustavě zapisuje jako 1,1 to asi víš i sám
Čili po prvním roce při inflaci 10% budeš mít MAJETEK / 1,1 , ale další rok budeš mít znova inflaci a ta inflace bude zase 10%, takže zase se ti zmenší majetek v tom stejném poměru jako jsou ty dvě úsečky A : B
=>
1 rok - MAJETEK / 1,1
2 rok - MAJETEK / 1,1 / 1,1
3 rok - MAJETEK / 1,1 / 1,1 / 1,1
atd atd atd, tu se předpokládá, že inflace je neustále 10% což znamená, že místo 110 ti zbyde jen 100, ta inflace se samozřejmě může ve skutečnosti každý rok měnit.
No a podobně když budeš něco násobit například 11/10 a to desetkrát po sobě, tak se to zapisuje nějak takto:
Podobně tak když budeš něčím dělit a to desetkrát po sobě, tak se to zapíše takto:
===========================================
Zkrátka inflace x% ti řekne, že hodnota peněz(správněji asi spíš hodnota Koruny) tento rok, poměřovaná hodnotou peněz další rok je (100+x)/100
Aby to nebylo málo absurdní, tak to číslo, kterého se dopočítáš ti samozřejmě neřekne, kolik ti ubude mincí, mincí budeš mít fyzicky za 20let pořád stejně, ale jejich hodnota klesne. Čili v tvým případě nyní máš 1 500 000 Kč, za 20 roků budeš mít samozřejmě znova stejné množství Kč, tedy 1 500 000 Kč, ale jejich hodnota bude taková, jako je hodnota 915406,4143 Kč v současnosti.
Čili 1 Kč bys měl jak se zdá brát jako hodnotu majetku, tedy né jako Korunu v peněžence, ale co si za tu Korunu můžeš pořídit majetku, tedy kolik Koruna představuje majetku.
Možná by to šlo líp ukázat na převodu jednotek, že pokud se ti z 1000 metrů stane 1000 centimetrů, tak je jasné, že máš 100krát méně, přestože máš stále 1000.
1000 metrů = 1000 ×(100×cm) => když délku podělíš stem => buď můžeš napsat, že máš při poměření k metru 10 metrů nebo máš stále 1000 ale už 1000cm.
Snad je na tom vidět, že tam nejde o tu měrnou jednotku, ale o tu skutečnou délku, která se zkrátí, stejně tak u hodnoty majetku nejde při inflaci o to, zda majetek poměřuješ ke Koruně nyní nebo ke Koruně za 5 let, ale jde o tu hodnotu majetku.
Pokud chceš být správný ekonom, tak samozřejmě nemůžeš lidem říct, že za 5 let budou mít stále 1 500 000, ale že budou mít tolik ve vztahu ke "Koruně za 5 let", protože lidé neznají hodnotu Koruny za pět let, musíš je nakrmit nějakou "mírou majetku"(míra ve smyslu Kč, €, $), kterou dobře znají, tedy znají její hodnotu - jak by se laicky řeklo, znají hodnotu peněz (teda někteří :) ). Proto bys měl tu budoucí hodnotu majetku vyjádřít ke Koruně v součastnosti, jelikož lidé používající Koruny, žádnou jinou hodnotu platidla neznají a nedokáží si ji lehce představit, teda alespoň se mi zdá, že se to celé alespoň trochu podobá pravdě.
Offline
#7 17. 08. 2012 18:18
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Inflace po 20 rokoch
↑ peter_2+2: ja tomu chápem, len nejde mi tento priklad vypočítať
Offline
#8 17. 08. 2012 20:55
Re: Inflace po 20 rokoch
↑ miso16211:
Vždyť jsi ho vypočítal a správně, jen jsi se ptal, proč je tam "-", ono tam žádné mínus není, takže všichni tu předpokládali, že myslíš "-" jakožto stát se menším :O.
Takže vše chápeš ale nevíš jak to vypočítat, je to podobné jako vědět proč sekyrka a jak seká dříví, jaký je ten správný pohyb, ale ještě nemít praxi v sekání :O? Asi to bude v těch přidružených věcech, které doprovází jednu činnost, je to dělení nebo násobení nebo která z těch?
Nedává mi to zatím smysl, zatímco ty jsi ve stavu chápání, mě jsi uvedl do stavu nevědomí :O.
Vžij se taky do situace nás nechápavých, určitě jsi v té situaci už taky někdy byl nebo jsi se jí alespoň dotýkal a pokus se nám vysvětlit co ti nejde a my se ti potom pokusíme pomoct :o. Teda pokud máš stále pocit, že to sám nezvládneš.
Offline
#9 18. 08. 2012 01:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Inflace po 20 rokoch
Zdravím v tématu,
v textu vidím 2 vzorce pro výpočet budoucí hodnoty: (1)
(1)
a (2).
(2).
Předpokládám, že mám 1000 Kč a roční míra inflace je 1 %.
Pomocí obou vzorců se dostávám k cca stejnému výsledku, ovšem první vzorec bych vyložila jako "bázová hodnota" je hodnota následujícího roku (100 %) a hodnota předchozího roku k bázové je vyšší a činí 101 %. Naopak 2. vzorec bych vyložila, že "bázová hodnota" je hodnota předchozího roku (100 %) a hodnota následujícího roku je nižší a k bázové činí 99 %.
Je možné, že to lépe osvětlí někdo z místních ekonomů, v každém případě nic nedáme za dotaz přímo na pana Krynického, proč v jednom textu používá 2 různé vzorce.
Offline
#10 18. 08. 2012 08:12
Re: Inflace po 20 rokoch
↑ jelena:
Zdá se mi, že pokud ten druhý vzorec není pouze teoretický (stím prvním jsem se už setkal, takže ten by měl být snad skutečný), pak při tom jak jsi oba vzorce přehledně shrnula, a vedoucí k různým výsledkům, by musely existovat i dvě různé hodnoty inflace.
Jak říkáš, raději si počkáme na nějakého ekonoma, snad někdo poradí.
Offline
#11 18. 08. 2012 11:07 — Editoval miso16211 (18. 08. 2012 11:23)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Inflace po 20 rokoch
1 500 000
po 1. roku hodnota 
po 2. roku hodnota 
Toto je asi ten prvy vzorec
po 20 roku 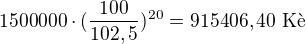
Ale Krynický uvádza hodnotu 904 031, 50 Kč. Pravdepodobne použil druhý vzorec. Ako to funguje?
Kedy používam ten druhý vzorec?
Offline
#12 18. 08. 2012 11:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Inflace po 20 rokoch
↑ miso16211:
Zdravím, Mišo,
na 2 vzorce upozorňuje i ↑ Pavel Brožek:. Pokud se na úvod zavedl jeden vzorec pro výpočet budoucí hodnoty, tak ten vzorec podle mne by měl být použit po celou sbírku (zejména, když u 2. vzorce není žádný komentář).
Takových postupů výpočtu může být více - viz metodiky ČSÚ. proto je dobré ohovořit, který vzorec bude použit.
Můžeš sám odvodit, k jakému poměru budoucích hodnot se dostaneš, když podělíš 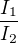 (I dle 1. vzorce a dle 2. vzorce).
(I dle 1. vzorce a dle 2. vzorce).
Mišo napsal(a):
Ale Krynický uvádza hodnotu 904 031, 50 Kč. Pravdepodobne použil druhý vzorec. Ako to funguje?
Kedy používam ten druhý vzorec?
To jsem popsala v příspěvku - záleží, který rok budeš používat jako bázový. Ale napiš, prosím, přímo panu Krynickému - má možnost diskuse.
↑ peter_2+2:
já jen, že Ty se opět pouštíš do rozsáhlých výkladů, aniž bys pořádně přečetl, v čem je problém autora dotazu.
peter_2+2 napsal(a):
jen jsi se ptal, proč je tam "-", ono tam žádné mínus není, takže všichni tu předpokládali, že myslíš "-" jakožto stát se menším :O.
Část přispívajících v tématu "minus" ve 2. vzorci vidí, tedy, prosím, negeneralizuj.
Offline
#13 18. 08. 2012 19:29
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Inflace po 20 rokoch
↑ jelena:
chcel bych pomoct panovi Krynickemu, ale nejde to nijak, poslal som mu mail - neodpovedano, nemôžem sa ani registrovať na stranke realisticky.cz,
teda v jednom pdf pan Krynycky použil dva vzorce.
Nechápem tomu bázovy rok(zrejme raz sa použije 19 rokov raz 20 rokov, alebo niečo iné?). Ale nevadí.
Offline
#14 18. 08. 2012 20:04
Re: Inflace po 20 rokoch
↑ miso16211:
Jestli se spokojíš s tím, že kdy používat jaký vzorec(což byla tvá otázka), tak jeden z těch dvou vzorců je nesmysl, takže tohleto můžeš pustil z hlavy, nejspíš ten druhý neexistuje.

 <--- tenhle vzoreček s nejvyšší pravděpodobností neexistuje
<--- tenhle vzoreček s nejvyšší pravděpodobností neexistuje Offline
#15 18. 08. 2012 20:44
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Inflace po 20 rokoch
↑ miso16211:
Ahoj Míšo,
pročetl jsem si tu kapitolu a byl jsem stejně zmatený jako ty, nakonec jsem došel k tomu, že v úloze 6 je chyba.
To, že inflace je např. 2,5% víš, co znamená, to už tu padlo mnohokrát.
Peníze, které mám, ztratily nějakou část svojí hodnoty. V tomto případě 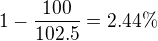 (milá teta opravila zápis v TeX :-)
(milá teta opravila zápis v TeX :-)
A tyto dvě veličiny pan Krynický v této úloze nejspíše zaměnil/špatně pojmenoval...
Jsou to jenom domněnky, ale podle uvedeného postupu to dává smysl (GP, kterou použil, se podobá poklesu hodnoty přístroje kvůli zastarávání).
↑ peter_2+2:
Ahoj,
jen mimochodem, co znamená sousloví "s nejvyšší pravděpodobností?"
Děkuji. A omlouvám se za vpadnutí do velmi plodného tématu :-)
Offline
#16 18. 08. 2012 21:00
Re: Inflace po 20 rokoch
Offline
#17 19. 08. 2012 00:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Inflace po 20 rokoch
↑ miso16211:
"Bázovým rokem" označuji rok, ve kterém je hodnota peněz považována za 100 % (a od tohoto roku počítám dál). Sleduj v textu - před Příkladem 1 je uvedeno:
pan Krynický napsal(a):
V následujících výpočtech ode všech podrobností odhlédneme a budeme uvažovat, že inflace znamená stejnoměrné znehodnocování peněz bez ohledu na dopad pro konkrétní druhy zboží. Pokud je roční míra inflace 3% znamená to, že se ceny v za rok v průměru zvýší o 3% ⇒ zboží, které stálo na začátku roku 100 Kč bude na konci roku stát 103 Kč.
Z tohoto pohledu na začátku roku bys měl k 100,- korun, co máš, přidat ještě 3 koruny a tak uložit si do šupliku, abys i na závěr roku mohl koupi stejné zboží, které dnes kupuješ za 100 korun. Nebo to zboží můžeš zakoupit již dnes za 100 korun. Toto vyjadřuje vzorec  .
.
---------------------------------------------------
peter_2+2 napsal(a):
Kde jsem podle tebe se mohl dočíst, mimo mého posledního dotazu a odpovědi na něj, co tím miso vlastně myslel?
Pokud bys ihned na úvod položil dotaz "Mišo, kde "tam" je to minus?" a počkal si na odpověď.
peter_2+2 napsal(a):
Kdo podle tebe ještě myslel, že miso pod oním "-" myslel mínus ve vzorci mimo tebe?. Jsi si jistá, že Pavel Brožek neodpovídal Geronimovi?
Já jsem nenapsala "myslel", ale "viděl": "Část přispívajících v tématu "minus" ve 2. vzorci vidí, tedy, prosím, negeneralizuj."
Pavel B. minus nejen viděl, ale dokonce ho opsal do vzorce v příspěvku ↑ Pavel Brožek: (kdyby neviděl pdf, tak by to nešlo).
↑ Hanis:
plodné to je - jediným užitečným výstupem je, že jsem Tobě opravila zápis v TeX (přidáno \ před %).
Offline
#18 19. 08. 2012 09:59 — Editoval peter_2+2 (19. 08. 2012 10:15)
Re: Inflace po 20 rokoch
Offline
#19 19. 08. 2012 12:18
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Inflace po 20 rokoch
↑ miso16211:
Ještě ke komunikaci s panem Krynickým - je období prázdnin, je možné, že je mimo dosah. Můžeš ještě zkusit kontakt ze staré stránky - možná funguje.
↑ peter_2+2:
:-)
Míšo v úvodním příspěvku jasně napsal, že konzultuje úlohu 6. V úloze je jen jedno minus.
Nevím kde bereš tu jistotu, že opravdu myslel mínus ve vzorci. Skoro se zdá, že řídíc se tvými radami a postupy, bych ti musel doporučit vždy se prvně misa zeptat, než začneš odpovídat a vyvozovat důsledky a psát dlouhosáhlé příspěvky :P.
Přesně tak - dokonce to dost často i dělám - buď požaduji upřesnění zadání, nebo přímo donesu možný text zadání. Dost to navazuje i na styl mého působení v reálu.
Takže kdyby jsi někoho poslala pro hrábě "tam" a on se vrátil, že "tam" žádné hrabě nejsou, začala by jsi ho osočovat z generalizace, že "tam" někdo nějaké hrabě vidí?
Já bych neposlala "tam", já bych poslala velmi adresně.
Generalizaci jsem nerozuměla slovo "tam", ale slovo "všichni", které jsem dokonce vytučnila v citátu.
Skoro se taky zdá Jeleno, že nesnášíš sama sebe, přitom umíš být tak hodný a milý člověk, když se trochu snažíš :O.
nepotřebuji být hodná a milá, tedy ne v tom smyslu, v jakém si to Ty možná představuješ. Např. na Mišo jsem asi byla tvrdá, ale už se hodně vylepšil ve formulací svých matematických problémů, ještě má dost práce, aby formulace byla natolik srozumitelná a jednoznačná, aby se problému ujmul někdo z opravdových autorit. Protože pro Mišo to smysl má.
Co nemá smysl - pouštět se do internet-diskusí s účastníky Tvého typu a ztrácet takto čas - žehlení je daleko přínosnější. Zkus pochopit styl debat, který podporuji "jasná formulace problému = adresná, konkrétní a srozumitelná odpověď". Zůstávám s pozdravem
zlá a protivná Jelena.
Offline
#20 19. 08. 2012 16:21 — Editoval peter_2+2 (19. 08. 2012 16:43)
Re: Inflace po 20 rokoch
Offline
#21 19. 08. 2012 19:34
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Inflace po 20 rokoch
↑ peter_2+2:
Reagoval jsem na úvodní příspěvek, svůj příspěvek jsem editoval, aby to bylo zřejmé. (Netuším, jestli tato informace má pro vaši debatu nějaký význam, a radši to ani nechci vědět, abych nebyl do debaty zapojen. :-D)
Offline
#22 19. 08. 2012 19:59
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Inflace po 20 rokoch
Za poslední 3 roky jsem se s inflací něco málo napočítal a "druhý" vzorec jsem v životě neviděl.
Neříkám, že neexistuje, jen jsem ho opravdu nepoužil. Ani mi nedává smysl.
Offline
#23 19. 08. 2012 20:39 — Editoval peter_2+2 (19. 08. 2012 20:47)
Re: Inflace po 20 rokoch
↑ Pavel Brožek:
Ve skutečnosti má i nemá.
Jestli jsi fakt poznal, že tím mínusem v prvním příspěvku myslel miso mínus ve vzorci a neodpovídal jsi tím "jen" na dva různé výsledky, o kterých mluvil na jedné straně miso a na druhé straně geronimo, pak to ukazuje, že jsem se spletl a opravdu si všichni nemysleli, že tím mínusem miso myslí to, že po inflaci se stane hodnota majetku nižší.
Ale to jádro diskuse je o obecné věci, takže je to spíš zajimavá informace, jak to vlastně nakonec bylo.
_______________
Jinak podle mě ta diskuse měla být označena za zodpovězenou až teď po příspěvku Halogana.
Offline
#24 24. 08. 2012 00:18
Re: Inflace po 20 rokoch
Vzorec s mínusem je špatný. Jde o chybu, která se při výpočtu inflace vyskytuje docela často (takto mě ji učili počítat) a obsahovala ji i původní verze učebnice. To o čem jste diskutovali, byl nějaký přechodný tvar, aktuální verze chybu opravuje a zmiňuje i špatný vzorec.
Offline
