Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Kombinatorická úloha (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 08. 2012 15:01 — Editoval BakyX (26. 08. 2012 15:03)
Kombinatorická úloha
Dobrý deň. Skúste si túto zaujímavú úlohu:
Uvažujme množinu  . Nech
. Nech  je ľubovoľná podmnožina
je ľubovoľná podmnožina  s počtom prvkov aspoň
s počtom prvkov aspoň  . Dokážte, že existuje prvok
. Dokážte, že existuje prvok  taký, že
taký, že  .
.
1^6 - 2^6 + 3^6 = 666
Offline
- (téma jako vyřešené označil(a) BakyX)
#2 27. 08. 2012 19:29 — Editoval vanok (27. 08. 2012 21:14)
Re: Kombinatorická úloha
Ahoj ↑ BakyX:,
Édit +korekcia nepozornosti vdaka poznamke BakyX
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 27. 08. 2012 20:04 — Editoval BakyX (27. 08. 2012 20:10)
Re: Kombinatorická úloha
1^6 - 2^6 + 3^6 = 666
Offline
#4 27. 08. 2012 21:16
Re: Kombinatorická úloha
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 30. 08. 2012 13:17 — Editoval vanok (30. 08. 2012 19:29)
Re: Kombinatorická úloha
Pozdravujem ↑ BakyX:,
Akoze nikdo nenapisal riesenie tak tu davam moje
Poznamka, BakyX, ty mas iste ine riesenie, mozes ho nam tu popisat.
Edit: Korekcia urobena, vdaka poznamkam, kolegu anes, ktoremu dakujem.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 30. 08. 2012 15:46
- check_drummer

- Příspěvky: 4638
- Reputace: 99
Re: Kombinatorická úloha
↑ vanok:
Ahoj, z čeho prosím plyne, že je Tebou uvedná množina maximální taková?
Děkuji
"Máte úhel beta." "No to nemám."
Offline
#7 30. 08. 2012 16:32 — Editoval vanok (30. 08. 2012 16:32)
Re: Kombinatorická úloha
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 30. 08. 2012 17:28 — Editoval anes (30. 08. 2012 17:56)
Re: Kombinatorická úloha
Ahoj,
↑ vanok:
↑ check_drummer:
Naprosto analogickým odůvodněním ta maximální množina půjde konstruovat i odzadu
Můžeme uvažovat tak:
EDIT:
↑ vanok:
Tady podle mě vypadlo ještě 23 členů za čísla tvaru 64a, takže se to nasčítá na 1999.
Offline
#9 30. 08. 2012 18:54 — Editoval vanok (30. 08. 2012 19:18)
Re: Kombinatorická úloha
↑ anes:
Ahoj, dakujem ze ta tento problem, a specialne moje risenie zaujalo.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 30. 08. 2012 19:52
- check_drummer

- Příspěvky: 4638
- Reputace: 99
Re: Kombinatorická úloha
↑ vanok:
Pak je ovšem otázka, zda všechny takové maximální množiny mají stejný počet prvků...
"Máte úhel beta." "No to nemám."
Offline
#11 30. 08. 2012 20:35
Re: Kombinatorická úloha
Ahoj ↑ check_drummer:,
Dufam, ze ano. No na dokaz nemam zatial myslienky.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 31. 08. 2012 16:54
- check_drummer

- Příspěvky: 4638
- Reputace: 99
Re: Kombinatorická úloha
Ahoj,
napadlo mě toto (většina toho co napíšu ale už bylo řečeno výše, spíš to řeknu trošku jinak). Rozdělme M na třídy ekvivalence. Každá třída je maximální taková množina prvků {xi}, že  .
.
Je zřejmé, že:
- nejmenším prvkem každé třídy je liché číslo
- k "porušení" podmínky (říkejme této podmínce P), že daná množina B,  , neobsahuje prvky x a 2x dojde pro nějaké dva prvky jedné třídy ekvivalence
, neobsahuje prvky x a 2x dojde pro nějaké dva prvky jedné třídy ekvivalence
Tedy pro nalezení maximální množiny B, která neporušuje P, stačí hledat maximální množinu neporušující P v každé třídě ekvivalence. To je však jednoduché. Každá taková tříde je totiž tvaru {y,2y,4y,.., } pro y liché. Tj. stačí do B vložit např. každý 1.,3.,5.,... prvek (pokud je počet prvků dané třídy sudý, pak by bylo možné do B vložit i každý 2.,4.,6.,... prvek).
} pro y liché. Tj. stačí do B vložit např. každý 1.,3.,5.,... prvek (pokud je počet prvků dané třídy sudý, pak by bylo možné do B vložit i každý 2.,4.,6.,... prvek).
Teď jde jen o to vhodně spočítat počet těchto prvků. Rozdělíme třídy ekvivalence na podtřídy obsahující stejný počet prvků - tedy lze z každé takové třídy vložit do B stejný počet prvků (n) a je-li tříd v dané podtřídě k, pak tato podtřída přispěje do B celkem n.k prvky. Totéž provedeme pro všechny podtřídy a výsledek sečteme.
Např. třídy obsahující jen jeden prvek jsou třídy, jejichž první prvek je mezi 1501 a 3000 (a je to liché číslo), podobně třídy obsahující právě dva prvky jsou třídy, jejichž první prvek je mezi 751 a 1500, atd.
Tj. celkem máme třídy tyto třídy (v závorce je vždy počet tříd, počet znamená počet prvků každé třídy a tot je celkový počet prvků, kterým třídy o těchto prvcích souhrnně přispívají do B):
1501-3000 (750), počet 1, tot 750
751-1500 (375), počet 2, tot 375
376-750 (187), počet 3, tot 374
188-375 (94), počet 4, tot 188
94-187 (47), počet 5, tot 141
47-93 (24), počet 6, tot 72
24-46 (11), počet 7, tot 44
12-23 (6), počet 8, tot 24
6-11 (3), počet 9, tot 15
3-5 (2), počet 10, tot 10
2-2 (0), počet 11, tot 0
1-1 (1), počet 12, tot 6
celkem: 1999
Tedy množina obsahující 2000 prvků již poruší podmínku P.
Pokoušel jsem se uvedený počet vyjádřit nějak elegantněji, ale problém zde nastává s tím, že počet tříd v každé podtřídě závisí na tom, zda je první číslo uvedeného intervalu liché nebo sudé: Např. v případě tříd, které obsahují 10 prvků, začínají tyto třídy (resp. jsou to jejich nejmenší prvky) číslem 3 až 5. jelikož číslo 3 je liché, máme dvě třídy s 10 prvky (obsahující 3 a 5). Pokud by však např. tyto třídy začínaly čísly 2 až 4, pak bychom měli jen jednu třídu (začínající 3).
Obecně tedy pro třídu obsahující i prvků máme dolní a horní hranici pro nejmenší prvek každé takové třídy jako: ![kopírovat do textarea $[\frac{|M|}{2^i}]+1$](/mathtex/16/1638cddd68d69be126ff3a3ddc4e751a.gif) až
až ![kopírovat do textarea $[\frac{|M|}{2^{i-1}}]$](/mathtex/05/05422183da2dad440e4a4a8bdb4b5d67.gif) , tedy počet lichých čísel v tomto intervalu je
, tedy počet lichých čísel v tomto intervalu je ![kopírovat do textarea $k_i := [\frac{ [\frac{|M|}{2^{i-1}}] - [\frac{|M|}{2^i}] + c}{2}]$](/mathtex/75/75a8ba788152e00e9f5a284b8ce0fca9.gif) , kde c=1 pro
, kde c=1 pro  liché, jinak je c=0.
liché, jinak je c=0.
Počet prvků z každé této třídy, které mohou přispět do B je ![kopírovat do textarea $n_i := [\frac{i+1}{2}]$](/mathtex/7d/7d9ae3c386623162010117561b57c4a6.gif) , tedy celkem je počet prvků přispívajících do B dán jako
, tedy celkem je počet prvků přispívajících do B dán jako  , kde sčítáme dokud hranice některé ze tříd není číslo 1.
, kde sčítáme dokud hranice některé ze tříd není číslo 1.
Velice zhruba řečeno jde tedy o sumu tvaru  .
.
"Máte úhel beta." "No to nemám."
Offline
#13 31. 08. 2012 19:55
Re: Kombinatorická úloha
Ahoj ↑ check_drummer:,
Cize si dokazal ( Ako aj anes), ze "maximalne " mnoziny nemusia mat tu istu kardinalitu.
Jednoducho som ten nazov som spante vybrat.
Navrh mena "CUDZIA" mnozina.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 17. 09. 2012 15:48
Re: Kombinatorická úloha
Dobrý deň. Ďakujem za zaujímavú diskusiu. Konečne som späť a preto načrtnem moje riešenie:
Všetky čísla z množiny  rozdeľme do tried tak, že v každej z nich budú čísla tvaru
rozdeľme do tried tak, že v každej z nich budú čísla tvaru  pre konkrétne nepárne
pre konkrétne nepárne  . Ak si vezmeme čísla z dvoch rôznych tried, tak zrejme ich podiel nie je celočíselný, alebo je deliteľný nepárnym číslom a teda je rôzny od 2. Preto stačí určiť, koľko najviac čísel možno zobrať z každej triedy, čo je už len počítanie.
. Ak si vezmeme čísla z dvoch rôznych tried, tak zrejme ich podiel nie je celočíselný, alebo je deliteľný nepárnym číslom a teda je rôzny od 2. Preto stačí určiť, koľko najviac čísel možno zobrať z každej triedy, čo je už len počítanie.
Skrátka prakticky to isté, ako má ↑ check_drummer:.
Odvádzal som aj všeobecný vzorec pre maximálny počet prvkov tejto podmnožiny ak  má ako prvky prvých
má ako prvky prvých  čísel a je celkom hrozivý:
čísel a je celkom hrozivý:
Pre  to však po troške počítania hádže
to však po troške počítania hádže  .
.
1^6 - 2^6 + 3^6 = 666
Offline
#15 17. 09. 2012 20:08
Re: Kombinatorická úloha
Mala poznamka: Riesenie ↑ vanok:, ma zabavnu formu, ak je napisane v dvojkovej sustave.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Kombinatorická úloha (TOTO TÉMA JE VYŘEŠENÉ)

 kde
kde  je nepárne máme
je nepárne máme  .
. ( ktora nam povoli "vyrobit" mnoziny
( ktora nam povoli "vyrobit" mnoziny 




 clenov.
clenov. cisiel z
cisiel z  , je vdaka konstrukcii dvojnasobok nejakeho cisla z
, je vdaka konstrukcii dvojnasobok nejakeho cisla z  kde
kde vyhovuje a ma
vyhovuje a ma  je buď dvojnásobkem, nebo polovinou něčeho z
je buď dvojnásobkem, nebo polovinou něčeho z  . Zvolením
. Zvolením 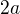 , ale na zbytek čísel už žádné podmínky nenakládáme, takže ho do
, ale na zbytek čísel už žádné podmínky nenakládáme, takže ho do  , pak
, pak  a
a  , a dál, dokud neprobereme všechna čísla do 3000.
, a dál, dokud neprobereme všechna čísla do 3000. obsahovat nanejvýš 2/3. Podobně pokračujeme se zbytkem.
obsahovat nanejvýš 2/3. Podobně pokračujeme se zbytkem.