Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vlastnosti koeficientu korelace (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 10. 2012 10:53
Vlastnosti koeficientu korelace
Ahojte,
prosím o pomoc s následujícím:
Je známý koeficient korelace mezimezi náh. veličinami A a B (např. 0,38), dále mezi veličinami A a C (0,67).
Je možno na základě těchto známých údajů prohlásit něco o korelaci mezi veličinami B a C? Pokud ano/ne, z čeho to plyne?
Děkuji a zdravím.
Offline
- (téma jako vyřešené označil(a) jelena)
#4 26. 10. 2012 23:59 — Editoval Brano (27. 10. 2012 00:13)
Re: Vlastnosti koeficientu korelace
Otazka je dobre polozena. Teda predpokladam, ze to su jedine informacie ktore mame. Nuz tazko mi je tu pisat nejaku radu ... napisem rovno riesenie.
Nech


potom a oznacme
a oznacme  , podobne
, podobne  . Vsimni si, ze sa naozaj jedna o skalarny sucin a mozeme si teda
. Vsimni si, ze sa naozaj jedna o skalarny sucin a mozeme si teda 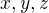 "predstavovat" ako vektory v
"predstavovat" ako vektory v 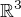 .
.
Vsimni si, ze  ... ta prva rovnost je definicia oznacenia
... ta prva rovnost je definicia oznacenia  - teda NEMYSLIM tym druhu mocninu tej nahodnej premennej ale jej disperziu.
- teda NEMYSLIM tym druhu mocninu tej nahodnej premennej ale jej disperziu.
Rovnako aj  a
a  . Nech
. Nech  a
a  ... toto je tvoje zadanie.
... toto je tvoje zadanie.
Definujeme  a
a  , potom
, potom  ,
,  ,
,  ,
,  a
a  ,
,
kde  je kosinus uhla medzi
je kosinus uhla medzi  , alebo inymi slovami
, alebo inymi slovami  .
.
Teraz si vsimni, ze na to aby boli splnene podmienky zo zadania, tak  mozu byt lubovolne vektory z ortogonalneho doplnku k
mozu byt lubovolne vektory z ortogonalneho doplnku k  s patricnou dlzkou, cize
s patricnou dlzkou, cize  moze byt lubovolne z
moze byt lubovolne z ![kopírovat do textarea $[-1,1]$](/mathtex/f5/f5d766fbe82b7d375db132c40fdc0732.gif) .
.
Teda jedine co vieme povedat je, ze![kopírovat do textarea $r(B,C)=y\cdot z\in \left[pq-\sqrt{(1-p^2)(1-q^2)}\ ,\ pq+\sqrt{(1-p^2)(1-q^2)}\right]$](/mathtex/87/87e8c021f19ac40e601bb656a337f37d.gif) .
.
Este ako malu skusku spravnosti (skor taky "sanity check") si mozes overit, ze ten interval je podmnozina ![kopírovat do textarea $[-1,1]$](/mathtex/f5/f5d766fbe82b7d375db132c40fdc0732.gif) pre lubovolne
pre lubovolne ![kopírovat do textarea $p,q\in[-1,1]$](/mathtex/e8/e8500ade8dc170baede497a409d34722.gif) ... mne to vyslo.
... mne to vyslo.
PS: Urcite si vsetko poriadne skontroluj, ci som neurobil chybu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vlastnosti koeficientu korelace (TOTO TÉMA JE VYŘEŠENÉ)
