Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nalezněte matici lineárního zobrazení (TOTO TÉMA JE VYŘEŠENÉ)
#2 30. 11. 2008 11:04
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nalezněte matici lineárního zobrazení
Offline
#7 30. 11. 2008 11:29
Re: Nalezněte matici lineárního zobrazení
↑ kuba:
Báza je daná. Každý polynóm môžeš zapísať nasledovne:
Tento vektor sa zobrazí na vektor:
To znamená, že 
Teda potrebuješ nájsť takú maticu, aby platila rovnosť:
Už vieš ako pokračovať?
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#9 30. 11. 2008 11:46 — Editoval BrozekP (30. 11. 2008 11:48)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nalezněte matici lineárního zobrazení
↑ kuba:
Promiň, myslel jsem, že tě pouze zajímá, jestli to někdo vyřeší.
Pro matici zobrazení musí zřejmě platit
kde matice  je matice zobrazení, jsou souřadnice vzoru v bázi E a jsou souřadnice obrazu v bázi F. Čísla
je matice zobrazení, jsou souřadnice vzoru v bázi E a jsou souřadnice obrazu v bázi F. Čísla  se zjistí tak, že dosadíš do této rovnosti postupně všechny bázové vektory z E (tj. např. pro bázový vektor x dosadíš a=0, b=1, c=0), na levé straně provedeš násobení a dostaneš rovnost dvou matic. Ty se rovnají pokud se rovnají všechny jejich prvky.
se zjistí tak, že dosadíš do této rovnosti postupně všechny bázové vektory z E (tj. např. pro bázový vektor x dosadíš a=0, b=1, c=0), na levé straně provedeš násobení a dostaneš rovnost dvou matic. Ty se rovnají pokud se rovnají všechny jejich prvky.
↑ lukaszh:
Zobrazuje se pouze do 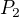 , ne
, ne 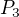 .
.
Offline
#10 30. 11. 2008 11:53
Re: Nalezněte matici lineárního zobrazení
↑ BrozekP:
No toš porad sem s toho jelen, chapu to co si napsal, ale co dal? nebo to už je vše? a k čemu tam je to F...
Offline
#11 30. 11. 2008 11:58
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nalezněte matici lineárního zobrazení
↑ kuba:
F je ze zadání - báze v 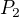 . Tak dokončím to pro bázový vektor x z E. V bázi E má souřadnice , jeho vzor má souřadnice . Dosadím do té rovnosti.
. Tak dokončím to pro bázový vektor x z E. V bázi E má souřadnice , jeho vzor má souřadnice . Dosadím do té rovnosti.
Na levé straně provedu násobení.
Z toho tedy dostávám  a
a  .
.
Ostatní čísla v matici zobrazení dostaneš tak, že dosadíš zbylé bázové vektory z E, tj. 1 a  .
.
Offline
#12 30. 11. 2008 12:12
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nalezněte matici lineárního zobrazení
↑ lukaszh:
Znovu jsem si přečetl tvůj příspěvek a nějak nechápu, co má znamenat
Vždyť to není dobře, správně by mělo být
Offline
#15 05. 12. 2009 17:11 — Editoval djsipic (05. 12. 2009 17:11)
Re: Nalezněte matici lineárního zobrazení
Ten vysledek je spravny, jednoduse je treba si to p(x) dat do matice a pak uz jenom prohodit horni a dolni pozice.
D(e1)=0+0x
D(e2)=1+0x
D(e3)=2x+4
.... pak hodit do matice :-) + prohodit ty pozice
0 1 4
0 0 2
.... uz je ti to trochu jasne? :-D
Offline
#16 12. 12. 2011 18:24
Re: Nalezněte matici lineárního zobrazení
Zdravim, pocitam si tu z knizky nejaky priklady na matice zobrazeni, princip je mi jakstaks jasnej, ale nevim, co znamenaj nektery symboly a co v nekterejch krokach delam.
pr:
zobrazeni z P1 do R3:
L(ax + b) = (2a-b,a+2b,3a-b)
baze P1:
p1(x)=x+1
p2(x)=2x-1
baze R3:
v1=(1,1,1)T
v2=(0,1,1)T
v3=(0,0,1)T
A ted tu mam: Matici linearniho zobrazeni L skladame po sloupcich ze souradnic L(p1) se striskou a L(p2) se striskou. Tedy:
L(p1) = L(x+1) = [1,2,3]T = .....
co vubec znamena to L(p1) se striskou?? to jsou souradnice ceho? zobrazene baze? nebo?
To same: co znamena L(p1)?? zobrazeni ceho kam??
dekuju
Offline
#17 13. 12. 2011 21:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nalezněte matici lineárního zobrazení
↑ hamii:
Zdravím,
ve vyřešeném tématu Tebe těžko někdo najde - je třeba si zakládat téma nové (případně s odkazem na další, pokud je pro Tebe použitelné a není třeba stejnou věc opakovat). Také je lepší umístit přímo náhled na materiál, ze kterého čerpáš - může to být jen interní označení, které zavedl Váš vyučující a je vysvětleno na úvod textu v seznamu označení (nebo také standardně využívané.
Ať se vede.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nalezněte matici lineárního zobrazení (TOTO TÉMA JE VYŘEŠENÉ)
