Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 11. 2012 18:10
Spojitosť funkcie v bode
Dobrý deň.
Je daná funkcia  definovaná v bode
definovaná v bode  , pričom
, pričom 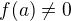 . Predpokladajme, že je v tomto bode spojitá. Ako dokázať, že v tomto bode je spojitá aj funkcia
. Predpokladajme, že je v tomto bode spojitá. Ako dokázať, že v tomto bode je spojitá aj funkcia 
Potrebujem to k dôkazu pravidla, že ak sú dve funkcie spojité v danom bode, tak v tom bode je spojitý aj ich podiel, preto to nemôžem použiť. Vopred ďakujem.
1^6 - 2^6 + 3^6 = 666
Offline
#3 02. 11. 2012 11:31
Re: Spojitosť funkcie v bode
Ahoj. Půjde to snadno i přímo, naznačím, jak na to.
Pro technické zjednodušení přidejme (v podstatě bez újmy na obecnosti) předpoklad  .
.
Odtud a ze spojitosti funkce  v bodě
v bodě  plyne, že pro body
plyne, že pro body  dostatečně blízké bodu
dostatečně blízké bodu  bude
bude  , takže
, takže  .
.
Stačí takto ?
Offline
#4 02. 11. 2012 14:21
Re: Spojitosť funkcie v bode
↑ Rumburak:
Ahoj. Ďakujem. Asi to chápem.
Na základe spojitosti  v
v  existuje
existuje  také, že pre
také, že pre  z okolia
z okolia  platí
platí  . Potom
. Potom  .
.
Predpokladáme, že je dané pevné  . Potom pre všetky
. Potom pre všetky  , pre ktoré platí
, pre ktoré platí platí aj
platí aj
Škoda, že som na niečo tak skvelé neprišiel sám. Dôkaz spojitosti  je v podstate rovnaký.
je v podstate rovnaký.
"dokaz, ze ak  je spojita v
je spojita v  a
a  je spojita v
je spojita v 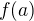 , tak
, tak  je spojita v
je spojita v  ."
."
Tak to absolútne netuším ako. O tej zloženej funkcii neviem ja osobne povedať nič, iba to, že je zložená z g, f.
1^6 - 2^6 + 3^6 = 666
Offline
#5 02. 11. 2012 16:27 — Editoval Rumburak (02. 11. 2012 16:42)
Re: Spojitosť funkcie v bode
↑ BakyX:
Tu druhou část důkazu nemáš úplně správně.
Máme tedy  takové, že pro každé
takové, že pro každé 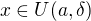 platí
platí  , takže též
, takže též
(1)  .
.
Nyní zvolme  a podívejme se na to z druhého konce. Když nalezneme
a podívejme se na to z druhého konce. Když nalezneme  takové, aby pro každé
takové, aby pro každé 
platilo
(2)  ,
,
bude podle (1) náš důkaz hotov. Ono  musíme hledat tak, aby pro každé
musíme hledat tak, aby pro každé 
- byla splněna nerovnost (1) - k čemuž stačí, aby ![kopírovat do textarea $\delta' \in (0, \delta]$](/mathtex/b4/b4cfcb7d621da27023cc0619b7ed7343.gif) (tuto úvahu máš ještě správně) ,
(tuto úvahu máš ještě správně) ,
- platila navíc nerovnost (2), kterou můžeme přepsat do tvaru
(3)  .
.
Pravá strana (3) (můžeme ji případně označit  ) je kladné číslo , takže odpovívající
) je kladné číslo , takže odpovívající  existuje, protože funkce
existuje, protože funkce 
je spojitá v bodě  . Avšak k doměnce, že se při tom uplatní podmínka
. Avšak k doměnce, že se při tom uplatní podmínka  , není žádný důvod.
, není žádný důvod.
***************
K důkazu spojitosti funkce  složené ze dvou spojitých - velmi stručný návod:
složené ze dvou spojitých - velmi stručný návod:
Bude-li  dosti blízko k
dosti blízko k  , bude i
, bude i  dosti blízko k
dosti blízko k 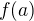 (protože
(protože  je spojitá) a potom také
je spojitá) a potom také 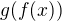 bude
bude
dosti blízko k 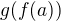 (protože
(protože  je spojitá). Ta "epsilon-delta gymnastika" tedy bude mít dvě logické úrovně.
je spojitá). Ta "epsilon-delta gymnastika" tedy bude mít dvě logické úrovně.
Všechny tyto důkazy se dají nalézt v každé vhodné učebnici (v české literatuře např. Vojtěch Jarník: Diferenciální počet I,
což je klasika).
Offline
#6 02. 11. 2012 19:08 — Editoval BakyX (02. 11. 2012 19:09)
Re: Spojitosť funkcie v bode
↑ Rumburak:
Aha...No tak to som teda dobrý idiot.
Už chápem, prečo je to moje riešenie zle. Chápem to takto: Keby náhodou to minimum bolo 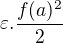 , tak medzi týmto minimom a
, tak medzi týmto minimom a  môžu ležať nejaké body, pre ktorú nemám zaistenú platnosť použitých odhadov. Chápem môj nedostatok správne ?
môžu ležať nejaké body, pre ktorú nemám zaistenú platnosť použitých odhadov. Chápem môj nedostatok správne ?
No a k tomu vášmu dôkazu. Stále niečo nechápem:
"Pravá strana (3) (můžeme ji případně označit  ) je kladné číslo , takže odpovívající
) je kladné číslo , takže odpovívající  existuje, protože funkce
existuje, protože funkce 
je spojitá v bodě  ."
."
No to existuje, avšak prečo bude menšie ako  ?
?
1^6 - 2^6 + 3^6 = 666
Offline
#7 02. 11. 2012 21:23
Re: Spojitosť funkcie v bode
↑ Rumburak:
To je v podstate presne technika dokazu, ze  je spojita. Teda je to vecou vkusu, ako si clovek chce utriast celu tu teoriu aby bola konzistentne podana.
je spojita. Teda je to vecou vkusu, ako si clovek chce utriast celu tu teoriu aby bola konzistentne podana.
Offline
#8 03. 11. 2012 11:10 — Editoval Rumburak (03. 11. 2012 11:27)
Re: Spojitosť funkcie v bode
Keby náhodou to minimum bolo
, tak medzi týmto minimom a
môžu ležať nejaké body, pre ktorú nemám zaistenú platnosť použitých odhadov.
Ano, to také. Ale zejména jde o to, že 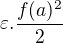 má - mnemotechnicky řečeno - vztah k ose y , zatímco ta různá hledaná
má - mnemotechnicky řečeno - vztah k ose y , zatímco ta různá hledaná 
mají analogický vztah k ose x.
"Pravá strana (3) (můžeme ji případně označit
) je kladné číslo , takže odpovívající
existuje, protože funkce
je spojitá v bodě."
No to existuje, avšak prečo bude menšie ako?
Když odhlédneme od předchozích úvah, tak ono  nalezené k číslu
nalezené k číslu  tak, aby na odpovídajícím okolí bodu
tak, aby na odpovídajícím okolí bodu 
platila sama nerovnost (3), ještě nemusí být menší nebo rovno  . My bychom to ale potřebobvali kvůli nerovnosti (2),
. My bychom to ale potřebobvali kvůli nerovnosti (2),
o níž se konstrukce důkazu opírá. Abychom toto zajistili, můžeme buďto vzít za "finální delta" číslo 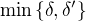 ,
,
nebo již hledání čísla  zpřísnit o podmínku
zpřísnit o podmínku  - tím se nic nezkazí.
- tím se nic nezkazí.
Offline
#9 03. 11. 2012 11:19 — Editoval Rumburak (03. 11. 2012 11:20)
Re: Spojitosť funkcie v bode
↑ Brano:
To je pravda. Mým záměrem bylo obejít se bez věty o spojitosti složené funkce, a to spíše z cvičných než praktických důvodů,
protože mi je jasné, že ona věta je důležitá i sama o sobě, takže ji nelze z matematiky vyškrtnout.
Offline
#10 03. 11. 2012 14:33
Re: Spojitosť funkcie v bode
↑ Rumburak:
Aha, chapem.
Inak ja som to myslel tak, ze by si BakyX dokazal tu vetu ako uzitocne cvicenie, nie ze by to obisiel iba odvolanim sa na dokaz niekde v ucebnici, kedze to vyzera, ze ma hlbsi zaujem o teoriu.
Offline
#11 03. 11. 2012 20:44
Re: Spojitosť funkcie v bode
↑ Brano:
Ja by som si to rád dokázal, ale skrátka...Som príliš hlúpy na to. Nejde mi to vôbec. Ide to úplne mimo mňa a budem rád, keď pochopím napísaný dôkaz.
Čo viem:
Pre ľubovoľné  existuje
existuje  také, že pre všetky
také, že pre všetky  , pre ktoré platí
, pre ktoré platí  , platí aj
, platí aj  .
.
Pre ľubovoľné  existuje
existuje  také, že pre všetky
také, že pre všetky  , pre ktoré platí
, pre ktoré platí  , platí aj
, platí aj  .
.
Prosím vás. Ukážte mi nejaký spôsob, ako z týchto vecí dostať toto:
Pre ľubovoľné  existuje
existuje  také, že pre všetky
také, že pre všetky  , pre ktoré platí
, pre ktoré platí  , platí aj
, platí aj  .
.
Fakt netuším ako na to, nemám knihu, kde by bol dôkaz a snažiť sa to dokázať sám už fakt nevládzem. Je to mimo mňa.
1^6 - 2^6 + 3^6 = 666
Offline
#12 03. 11. 2012 22:57 — Editoval Brano (03. 11. 2012 22:58)
Re: Spojitosť funkcie v bode
Podstata veci je v tom, ze sa nesmies stratit v oznaceniach - tie formalne zapisy sa snazia podat nejaku informaciu, ktoru podla mna chapes. A ta veta je intuitivne ocividna.
1. Ak  je blizko
je blizko  , potom
, potom  je blizko
je blizko 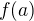 .
.
2. Ak  je blizko
je blizko  , potom
, potom 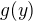 je blizko
je blizko  .
.
3. Dosadis 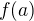 za
za  a
a  za
za  .
.
4. Dosledok: Ak  je blizko
je blizko  , potom
, potom 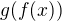 je blizko
je blizko 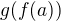 .
.
Skus to zapisat formalne, ak sa ti to nepodari, tak ti potom napisem riesenie.
Offline
#13 03. 11. 2012 23:43 — Editoval BakyX (03. 11. 2012 23:44)
Re: Spojitosť funkcie v bode
↑ Brano:
Tak intuitívne je to jasné od začiatku, je to vidieť aj zo spôsobu vykresľovania grafu zloženej funkcie...Lenže práve tá formálna stránka mi robí problém...Môže byť takto ? Tým mojím prvým krokom si nie som úplne istý.
Nech je dané  . Zo spojitosti
. Zo spojitosti  v bode
v bode 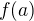 plynie, že existuje
plynie, že existuje  také, že pre všetky
také, že pre všetky  spĺňajúce
spĺňajúce  platí aj
platí aj  . (1)
. (1)
Nakoľko  je spojitá v
je spojitá v  , tak existuje
, tak existuje  také, že pre všetky
také, že pre všetky  pre ktoré
pre ktoré  platí aj
platí aj  . Pre tieto
. Pre tieto  z okolia
z okolia 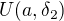 platí preto aj (1).
platí preto aj (1).
1^6 - 2^6 + 3^6 = 666
Offline
#14 04. 11. 2012 01:28
Re: Spojitosť funkcie v bode
Je to dobre. Ja by som to vsak prepisal s malou stylistickou upravou - nepisal by som "pre vsetky f(x)".
Njprv je fajn si napisat presne definicie, potom by nasledovala uvaha. Pre lubovolne
Pre lubovolne 
sa da najst  take, ze pre vsetky
take, ze pre vsetky  ; ak
; ak  potom
potom  . Dalej k
. Dalej k 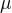 (tomu najdenemu)
(tomu najdenemu) existuje
existuje  taka, ze pre vsetky
taka, ze pre vsetky  plati; ak
plati; ak  potom
potom
 a tym padom
a tym padom 
 .
.
Cize mame spojitost  v
v  .
.
PS: snad ta "graficka" uprava nie je matuca.
Offline
#15 04. 11. 2012 01:47 — Editoval BakyX (04. 11. 2012 01:47)
Re: Spojitosť funkcie v bode
↑ Brano:
Som rád, že je to už dobre. Ďakujem. Ešte mám maličký problém zmieriť s tým dosadením 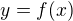 , ale to si už nejako v hlave urovnám.
, ale to si už nejako v hlave urovnám.
Ak sa môžem ešte spýtať, ako sa zvyčajne pomocou tejto definície dokazuje veta:
Ak  a
a  sú funkcie spojité v bode
sú funkcie spojité v bode  , tak aj
, tak aj 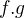 je funkcia spojitá v bode
je funkcia spojitá v bode  ?
?
1^6 - 2^6 + 3^6 = 666
Offline
#16 04. 11. 2012 02:12
Re: Spojitosť funkcie v bode
Pouzije sa  . V tom prvom clene sa potom odhadne
. V tom prvom clene sa potom odhadne  takto
takto  , kde
, kde  je z definicie spojitosti
je z definicie spojitosti  . Potom si uz iba staci uzrejmit, ze
. Potom si uz iba staci uzrejmit, ze  vie byt lubovolne male, t.j. ze pre lubovolne
vie byt lubovolne male, t.j. ze pre lubovolne  najdes
najdes  splnajuce
splnajuce  .
.
Akonahle by si robil anlyzu vektorovych funkcii viac premennych, tak by sa to dalo aj inak.
Offline
#18 04. 11. 2012 03:13 — Editoval BakyX (04. 11. 2012 05:23)
Re: Spojitosť funkcie v bode
↑ Brano:
Ďakujem za nový dôkaz. Vidím, že môj dôkaz "nie je ďaleko" od tohto. Ja som si definoval nové funkcie: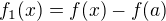
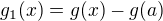
Z definície vidieť, že 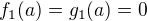 , preto veľmi ľahko dokážeme, že
, preto veľmi ľahko dokážeme, že 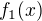 ,
,  ,
,  sú spojité v
sú spojité v  . Navyše, konštantná funkcia
. Navyše, konštantná funkcia 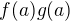 je spojitá v
je spojitá v  a tiež funkcie
a tiež funkcie 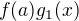 ,
, 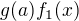 , preto je spojitý v
, preto je spojitý v  aj ich súčet, čo je
aj ich súčet, čo je 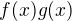 . No a k dôkazu spojitosti súčtu stačí použiť ten vzťah
. No a k dôkazu spojitosti súčtu stačí použiť ten vzťah 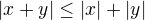 , čo ste použili aj vy.
, čo ste použili aj vy.
V tom vašom ste myslím použili aj odhad  a za finálne
a za finálne  vzali to menšie.
vzali to menšie.
↑ Brano: Tak toto ani lepšie povedať nedalo. Výstižná formulácia. S týmto vysvetlím už chápem, prečo je váš spôsob zápisu dôkazu lepší.
Ak sa smiem spýtať, ste vysokoškolský profesor ?
1^6 - 2^6 + 3^6 = 666
Offline
#20 04. 11. 2012 18:22 — Editoval vanok (04. 11. 2012 18:39)
Re: Spojitosť funkcie v bode
Ahoj ↑ BakyX:,
Len mala bibliograficka rada.
The Elements of Real Analysis, R.G. Bartle (Wiley )
I ked je to uz trochu starsia kniha, nic viac pedagogicke som este nevidel.
Dokonca je citatelna in line (pozri, ako prve, stranu 148 a nasledujuce)
http://fr.scribd.com/doc/32815810/Bartl … l-Analysis
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

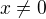 a dokaz, ze ak
a dokaz, ze ak