Matematické Fórum

user · 06. 11. 2012 19:35 — Editoval user (06. 11. 2012 22:24)

Ahoj,
mám problém s mocninnou řadou:
$\sum_{n=1}^{+\infty}\frac{x^n}{\lfloor\frac{n}2\rfloor!}$

$\rho=\frac1{\limsup \sqrt[n]{a_n}}$
Tak řeším limitu:
$\lim_{n\to+\infty}\frac{\lfloor\frac{n}{2}\rfloor!}{\lfloor\frac{n+1}{2}\rfloor!}$
Která mi pro n sudá vyjde 1, pro n lichá 0, takže bych dostal 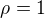$\rho=1$ .
Kde dělám chybu?

EDIT: Napadly mě ještě tyhle odhady:
$\sum_{n=1}^{+\infty}\frac{x^n}{\lfloor\frac{n}2\rfloor!}\le \sum_{n=1}^{+\infty}\frac{x^n}{\left(\lfloor\frac{n}2\rfloor\right)^{\frac{n}2}}\le \sum_{n=1}^{+\infty}\frac{x^n}{\left(\frac{n-1}2\right)^{\frac{n}2}}$
Odhadl jsem řadu shora konvergentní řadou pro všechna x, proto by měla konvergovat i původní řada.

Matematické Fórum

#1 06. 11. 2012 19:35 — Editoval user (06. 11. 2012 22:24)

Obor konvergence mocninné řady