Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 11. 2012 13:51
Geometrie - Shodná zobrazení
Dobrý den, potřeboval bych pomoct s následujícím příkladem: Jsou dány kružnice k_1 (O_1;4cm), k_2 (O_2;2,5cm), lO_1 O_2l je 3cm se protínají ve dvou bodech. Označte T jeden z průsečíků. Sestrojte všechny rovnostranné trojúhelníky ABC se základnou AB tak, aby platilo: A náleží k_1, B náleží k_2 a T byl těžiště trojúhelníka ABC.
Děkuju
Offline
#2 10. 11. 2012 14:36
Re: Geometrie - Shodná zobrazení
Ahoj.
Najprv dokáž, že uhol  má veľkosť
má veľkosť  .
.
Následne použiješ to, že otočením bodu  o
o  alebo
alebo  dostaneš bod
dostaneš bod  .
.
Otočíš preto jednu kružnicu okolo bodu  o
o  a
a  . Priesečník s druhou kružnicou je hľadaný vrchol ležiaci na nej. Spätným otočením nájdeš druhý vrchol.
. Priesečník s druhou kružnicou je hľadaný vrchol ležiaci na nej. Spätným otočením nájdeš druhý vrchol.
Dôkaz správnosti riešenia: Na základe konštrukcie máme  a
a  . Bod
. Bod  je preto stred kružnice opísanej rovnostranného trojuholníka
je preto stred kružnice opísanej rovnostranného trojuholníka 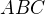 a preto je aj jeho ťažiskom.
a preto je aj jeho ťažiskom.
1^6 - 2^6 + 3^6 = 666
Offline
#3 10. 11. 2012 14:37 — Editoval Arabela (10. 11. 2012 14:38)
Re: Geometrie - Shodná zobrazení
Ahoj ↑ KajaHodik:,
všimnime si, že trojuholník ABC má byť rovnostranný s ťažiskom v bode T. Z toho vyplýva, že trojuholníky ATC a BTC sú rovnoramenné s vnútorným uhlom pri vrchole T s veľkosťou 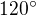 .
.
Hlavná myšlienka: Bod C je obrazom bodu A v otočení o 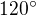 (resp.
(resp.  ) okolo bodu T. Keďže
) okolo bodu T. Keďže  , obraz bodu A v spomínanom otočení leží na obraze kružnice
, obraz bodu A v spomínanom otočení leží na obraze kružnice 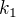 okolo bodu T. Obdobne s bodom B, len otáčanie kružnice
okolo bodu T. Obdobne s bodom B, len otáčanie kružnice  okolo bodu T bude v opačnom zmysle ako otáčanie kružnice
okolo bodu T bude v opačnom zmysle ako otáčanie kružnice 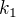 (o
(o  , resp. o
, resp. o 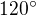 ).
).
Bod C dostávame ako prienik otočených kružníc ( ). Body A, B potom spätným otočením.
). Body A, B potom spätným otočením.
server.gphmi.sk/~domanyov
Offline

