Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Analytická geometrie- kružnice ze 3 bodů (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 12. 2008 17:06
- jerrycooper
- Zelenáč
- Příspěvky: 1
- Reputace: 0
Analytická geometrie- kružnice ze 3 bodů
Ahoj, mám fungující algoritmus na nalezení středu a poloměru kružnice ze 3 bodů. Mým problémem je, že mu moc nerozumím. Tady je algoritmus:
double m1 = (x1+x2)/2.0;
double n1 = (y1+y2)/2.0;
double m2 = (x1+x3)/2.0;
double n2 = (y1+y3)/2.0;
//System.out.println("Pulky: "+m1+","+n1+" "+m2+","+n2);
double c1 = (x2-x1)*m1 + (y2-y1)*n1;
double c2 = (x3-x1)*m2 + (y3-y1)*n2;
double mx = (x2-x1)*(y3-y1)+(y2-y1)*(x1-x3);
c_xs = (c1*(y3-y1)+c2*(y1-y2))/mx;
c_ys = (c1*(x1-x3)+c2*(x2-x1))/mx;
rs = java.lang.Math.sqrt((c_xs-x1)*(c_xs-x1)+(c_ys-y1)*(c_ys-y1));
Můj předpoklad je, že se vemou ty 3 body, udělají se 2 úsečky. Pak se vezmou osy těchto 2 úseček. Ve středu kružnice se protnou. Předpokládám, že výpočet c1 a c2 je vlastně vyjádření těch 2 os. Ale co je to mx a jaký je podklad pro dopočitání středu, to bych rád pochopil.
Něco podobného jsem našel tady, ale vysvětlené to taky není. Mohl by mě někdo vysvětlit princip těch 3 inkriminovaných řádků?
Offline
#2 15. 11. 2009 16:24
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Analytická geometrie- kružnice ze 3 bodů
![kopírovat do textarea $A[x_1,y_1]$](/mathtex/db/db56d2bb4b4e9a0aef15f120403ebb1f.gif)
![kopírovat do textarea $B[x_2,y_2]$](/mathtex/97/9743cf2f285919f8cb3202b8b20ebd40.gif)
![kopírovat do textarea $C[x_3,y_3]$](/mathtex/52/52004283e4820ba09d40ec014651ba47.gif)
![kopírovat do textarea $S_{AB}[m_1,n_1]$](/mathtex/2b/2b7c9aba9fb43b79c5b068985604f034.gif) je střed úsečky
je střed úsečky  .
.![kopírovat do textarea $S_{AC}[m_2,n_2]$](/mathtex/70/70c2bde7b592c670f97766d508c401ad.gif) je střed úsečky
je střed úsečky 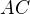 .
.![kopírovat do textarea $S[c_{xs},c_{ys}]$](/mathtex/9a/9aa10b7db26db017ab6673c81fbe038b.gif) je střed kružnice.
je střed kružnice.
Vektor  musí být kolmý na vektor
musí být kolmý na vektor  , stejně tak vektor
, stejně tak vektor 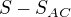 musí být kolmý na vektor
musí být kolmý na vektor  . Máme tak dvě rovnice
. Máme tak dvě rovnice
Po úpravě
Výrazy na pravé straně můžeme snadno spočítat a jak je vidět, jsou to čísla 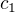 a
a  z algoritmu. Rozepíšu skalární součiny:
z algoritmu. Rozepíšu skalární součiny:
Spočtu si determinant soustavy (je vidět, že to je číslo 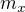 z algoritmu) a pomocí Cramerova pravidla dostávám přesně ty výrazy pro
z algoritmu) a pomocí Cramerova pravidla dostávám přesně ty výrazy pro  a
a 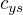 z algoritmu. Určení poloměru už snad nemusím komentovat.
z algoritmu. Určení poloměru už snad nemusím komentovat.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Analytická geometrie- kružnice ze 3 bodů (TOTO TÉMA JE VYŘEŠENÉ)