Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 01. 2013 11:16
Kvadratická rovnice s parametrem
Ahoj, opět si nevím rady s příkladem. s neznámou
s neznámou  a parametrem
a parametrem 
Nějak se mi nedaří dobrat se správného výsledku. Tentokrát ani nevím přesně, jak správně začít. Dle mého upravovat rovnici asi nemá význam.
Děkuji za jakoukoli radu.
Offline
- (téma jako vyřešené označil(a) bejf)
#6 10. 01. 2013 12:12
Re: Kvadratická rovnice s parametrem
↑ bejf:
ano, jenom potom nezapomeň zvlášť rozebrat případ 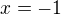
ano (i podruhé), potom je 
potom je
teoreticky bys to tak už mohl i nechat (s tím, že bys zvlášť pořešil případ 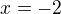 )
)
anebo můžeš ještě prodiskutovat případy  a
a 
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#7 10. 01. 2013 12:19
Re: Kvadratická rovnice s parametrem
↑ byk7:
Teď jsem chtěl napsat, že jsem na to přišel na ten výpočet, takže jsem to měl dobře, jen jsem si pak blbě dosazoval do vzorce pro výpočet kořenů.
A co se týče těch podmínek, ta pro x=-1 je jasná, ale pak je tam ax+2=0, pak tedy ax=-2, a ta neznámá na to nemá mít žádný vliv?
Offline
#8 10. 01. 2013 12:57
Re: Kvadratická rovnice s parametrem
↑ bejf:
jestliže rozebíráš nějakou konkretní hodnotu parametru, je dobré si za něj dosadit
to znamená, že pro 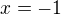 má rovnice
má rovnice  právě jedno řešení a to
právě jedno řešení a to 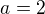
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#9 10. 01. 2013 13:19
Re: Kvadratická rovnice s parametrem
↑ byk7:
Rozumím, ale hned z toho nevyčtu, pro které hodnoty parametru má rovnice stejné řešení. Ta první hodnota 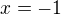 je jasná z první závorky, tu pak dosadím. Druhá závorka pak je
je jasná z první závorky, tu pak dosadím. Druhá závorka pak je  , a u té bych si chtěl ujasnit jednu věc - protože si z toho nemůžu nic vytknout, tak to pak můžu položit celé rovno nule
, a u té bych si chtěl ujasnit jednu věc - protože si z toho nemůžu nic vytknout, tak to pak můžu položit celé rovno nule  , tedy pak
, tedy pak  . Teď ale abych měl vyjádřené
. Teď ale abych měl vyjádřené  , tak by to mělo být
, tak by to mělo být  a tam se počítá pouze pro
a tam se počítá pouze pro 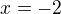 , tak z toho usuzuji, že ta neznámá
, tak z toho usuzuji, že ta neznámá  ve druhé závorce nemá žádný vliv na tu podmínku, resp. tu konkrétní hodnotu parametru, kterou mám dosazovat do původní rovnice. Je tak?
ve druhé závorce nemá žádný vliv na tu podmínku, resp. tu konkrétní hodnotu parametru, kterou mám dosazovat do původní rovnice. Je tak?
Offline
#12 10. 01. 2013 14:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kvadratická rovnice s parametrem
Zdravím v tématu. pro autora dotazu - zadání chybí co je třeba vyšetřovat. Standardní formulace takových úloh je:
Je dána kvadratická rovnice s neznámou  a parametrem
a parametrem  :
: 
Urči, pro které hodnoty parametru  :
:
a) rovnice má jen jeden kořen,
b) rovnice nemá žádný kořen,
c) rovnice má jeden dvojnásobný kořen,
d) rovnice má 2 různé kořeny,
e) rovnice má jeden nulový a jeden nenulový kořen atd.
Podaří se zorientovat? Začnete umístěním materiálu s teorii. Děkuji a zdar přeji.
Offline
#14 10. 01. 2013 14:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kvadratická rovnice s parametrem
↑ bejf:
děkuji, to v úvodním příspěvku nemáš. Tedy máš sestavit tabulku, ve které bude odpověď na otázky a) až d) ↑ příspěvek 12: + zápis kořenu ve formě a=f(x).
Offline
#16 10. 01. 2013 22:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kvadratická rovnice s parametrem
↑ bejf:
pořádně to snad zkontroluje kolega Ondra. Předpokládám, že komentář je soubor otázek a) až d).
Zatím jen výhrada k prvnímu řádku s D, úplně nakonec, kde se objevuje odmocnina,  odmocnina je až ve vzorci pro výpočet kořenů.
odmocnina je až ve vzorci pro výpočet kořenů.
Tedy diskutujeme možné  (nulové, kladné, záporné) - na výsledek to vliv nemá, ale pro jiné D by to vliv mělo i na výsledek.
(nulové, kladné, záporné) - na výsledek to vliv nemá, ale pro jiné D by to vliv mělo i na výsledek.
V ostatním jsem chybu nenašla.
Offline


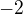 za
za 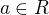 .".
.".