Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 28. 04. 2013 13:21
Re: Pravdepodobnosť
Myslím, že by se dalo vyjít z tohoto příkladu:
"Statistik dopravního podniku zjistil, že ve 20% vozidel MHD je černý pasažér. Kolik doprávních prostředků musí revizor skontrolovat aby na 95% našel alespoň jednoho."
Akorát musíš za 0,2 dát šanci na najde Jágra a výsledek pak vynásobit pěti. Tím bys měl získát počet kartiček, které musí koupit. Ovšem nerad bych tě uvedl v omyl, tak si to ještě někde ověř.
Offline
#4 28. 04. 2013 15:08 — Editoval Firejs (28. 04. 2013 15:09)
Re: Pravdepodobnosť
Ty logaritmy jsou součástí vzorečku, žádný předchozí výpočet neproběhl. Jediné co se tam mění je pravděpodobnost, kterou chceme a ta kterou máme. Tedy 0,95 a 0,2.
Vlastně tím spočítáš, kolik musí koupit karet aby na 95% měla alespoň jednoho Jágra...
Offline
#5 28. 04. 2013 17:28
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: Pravdepodobnosť
Ahoj,
priklad by som riesil nasledovne. Pravdepodobnost, ze najdem aspon 5 Jagrov v n kartach pocitam ako opacnu pravdepodobnost k tomu ze nenajdem ziadneho Jagra, najdem 1 alebo 2 alebo 3 alebo 4 Jagrov. Teda to bude 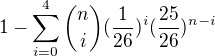
Podla binomickeho rozdelenia. Podla mna sa to neda tak zjednodusit ako psal ↑ Firejs:
To ze mam 95 percentnu sancu, ze najdem Jagra v n kartach, neznamena, ze potrebujem 5n kariet aby som ho tam nasiel s 95 percentnou sancou. Podla mna potrebujes vyriesit nerovnicu pre n
Inak ten takzvany vzorecek s logaritmama ↑ Firejs:, to je vysledok vypoctu
Pravdepodobnost, ze najdem aspon jedneho cierneho pasiaziera na n pokuseov, je opacna k pravdepodobnosti, ze nenajdem ziadneho cierneho pasaziera. a teda bude rovnat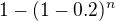
a my chceme 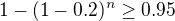
Po vyjadreni n, dostaneme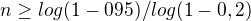
Offline
