Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 06. 2014 13:39
Exponenciální nerovnice
Zdravím. Měl bych dotaz ohledně jednoho příkladu. . Mám za úkol určit do jaké množiny reálných čísel spadá.
. Mám za úkol určit do jaké množiny reálných čísel spadá.
Postup:
Pro: x>0

 /
/ 
Příklady řeším graficky přes nulové body, takže tenhle krok přeskočím, protože nevím jak to sem nakreslit..
Vyjde: (-nekonečno, 0) u (1,+nekonečno)
Pro: x < 0

 /
/ 
Zase řešeno graficky..
Vyjde: (-nekonečno, -1) u (0,+nekonečno)
No a teďka bych měl sjednotit oba intervaly, které mně vyšli.. Což by teoreticky mělo být (-nekonečno, +nekonečno) ... Ale správně ve výsledcích je (-nekonečno, -1) u (1,+nekonečno).. Proč to tak je? Je to snad kvůli tomu, že jak jsem řešil přes ty nulové body, tak tam vlastně 1 a -1 nepatří ? Tím pádem vlastně ani 0 .. ?
Offline
- (téma jako vyřešené označil(a) Spalker)
#2 12. 06. 2014 13:50
- OndrasV

- Místo: Praha
- Příspěvky: 513
- Škola: VŠE (1997-2004), FEL (2014-??)
- Pozice: mudrlant
- Reputace: 31
Re: Exponenciální nerovnice
↑ Spalker: Ahoj, nemusíš tak komplikovaně. Použij, že  , tj.
, tj.  , tj. nerovnost platí, když x co?
, tj. nerovnost platí, když x co?
Offline
#3 12. 06. 2014 14:10
Re: Exponenciální nerovnice
ehm.. No, já to radši řeším takhle, protože jsme se to tak učili a žádnej jinej způsob neznám.. :) Navíc ačkoliv to vypadá zdlouhavě, tak to zas tak hrozný není, a pokud někde neudělám matematickou chybu, tak mně to vždycky vyjde.. Vím, že se snažíš pomoct, ale radši preferuju jistotu.. :).
Každopádně učit se různý zkratky / jiný rychlejší postupy se mně ani nechce, protože bych v tom měl pak akorát zbytečně guláš, zvlášť tomu tvýmu zápisu absolutně nerozumím :D ...
Jenom abych se vrátil k tomu na co jsem se ptal.. Je to (-nekonečno, -1) u (1,+nekonečno) kvůli těm nulovým bodům, nebo proč ten interval je takový a ne (-nekonečno, +nekonečno) ?
Offline
#4 12. 06. 2014 14:16
- misaH
- Příspěvky: 13460
Re: Exponenciální nerovnice
↑ Spalker:
Ahoj.
Keď dosadíš za x číslo 1, skúška nevyjde.
Offline
#5 12. 06. 2014 14:17
Re: Exponenciální nerovnice
↑ Spalker:
a to kvůli těm podmínkám
sám píšeš
Pro: x>0
Vyjde: (-nekonečno, 0) u (1,+nekonečno)
Takže průnik je 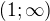
a podobně druhá varianta.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 12. 06. 2014 14:24
- misaH
- Příspěvky: 13460
Re: Exponenciální nerovnice
↑ Spalker:
Do tej najpôvodnejšej, lebo tú máš riešiť.
Offline