Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » PRIKLAD S KULICKAMA - Vytvorujici funkce, kombinatorika (TOTO TÉMA JE VYŘEŠENÉ)
#1 15. 06. 2014 10:48
- marketka01
- Příspěvky: 26
- Reputace: 0
PRIKLAD S KULICKAMA - Vytvorujici funkce, kombinatorika
Ahoj, pomuzete mi prosim s resenim tohoto prikladu? Nemam bohuzel spravny vysledek... Ale i tak, moc by mi pomohly vase reakce
Kolika zpusoby lze vybrat 60 kulicek tri barev (cervena,modra,zelena), kdyz soucet zelenych a modrych musi byt sudy ?
MOJE UVAHA JE NASLEDUJICI:
chapu, ze se to rozdeli na ty dva pripady, kdy
a) je lichy pocet Zelenych a Modrych,
b) sudy pocet Zelenych a Modrych
pritom Cervenych je vzdy pocet sudy
V pripadu b) to vychazi  a zajima me x^30 (ptz hledam dvojice, 60:2=30),
a zajima me x^30 (ptz hledam dvojice, 60:2=30),
v pripadu a) si to rozdelim na soucin  , je to dobre? A nevim jak dal,
, je to dobre? A nevim jak dal,
Rozdelila bych si to na casti, nejdriv bych vzala prvni zlomek v soucinu a tam bych hledala x^60, a u druheho zlomku by to bylo x^30
Pak bych to co mi vyjde mezi sebou vynasobila, a tim mi vyjde pocet zpusobu v pripadu za a)
Nakonec sectu pocet zbusobu v a) a b) a vysel by mi vysledek...
ALE OBAVAM SE ZE TO JE SPATNE :/
Offline
- (téma jako vyřešené označil(a) marketka01)
#2 15. 06. 2014 11:27 — Editoval Jj (16. 06. 2014 23:09)
Re: PRIKLAD S KULICKAMA - Vytvorujici funkce, kombinatorika
↑ marketka01:
Dobrý den, řekl bych (pokud jsem úlohu správně pochopil), že je-li počet červených sudý, pak součet
zelených a modrých musí být rovněž sudý (60 - sudý počet červených = sudý počet). Takže není třeba
dělení ad a) a b). Takže zjednodušení.
Je-li červených 58 může být zelených 1 1 možnost = 59 - 58
modrých 1
56 zelených 1 2 3 3 možnosti = 59 - 56
modrých 3 2 1
54 zelených 1 2 3 4 5 5 možností = 59 - 54
modrých 5 4 3 2 1
atd.
Takže pokud něco nepřehlížím, měl by být počet možností
Editováno:
Skryt zřejmě nesmyslný souhrn počtu možností.
Opraveno na

Pokud by mohl být počet zelených nebo modrých nulový (při dodržení podmínky sudosti součtu zelených a modrých),
přibyly by k danému počtu červených zřejmě vždy ještě dvě možnosti, tj.

Pokud se tedy nemýlím.
Offline
#3 15. 06. 2014 17:28
- marketka01
- Příspěvky: 26
- Reputace: 0
Re: PRIKLAD S KULICKAMA - Vytvorujici funkce, kombinatorika
↑ Jj:
diky za reakci, skoda ze nemam spravny vysledek
Ale hlavne mi jde o vyjadreni tou vytvorujici funkci, kdyby nekdo vedel jak na to , budu opravdu moc rada... sedim nad tim uz dlouho a porad se nemuzu dobrat nejakeho konce :/
Offline
#4 16. 06. 2014 16:39
- marketka01
- Příspěvky: 26
- Reputace: 0
Re: PRIKLAD S KULICKAMA - Vytvorujici funkce, kombinatorika
Nikdo netusi?? :(
Offline
#5 16. 06. 2014 17:17 — Editoval Brano (17. 06. 2014 13:23)
Re: PRIKLAD S KULICKAMA - Vytvorujici funkce, kombinatorika
keby si nemala ziadne obmedzenie na paritu, tak by ta vytvarajuca funkcia bola a hladala by si v nej clen pri
a hladala by si v nej clen pri 
teraz ak mas podmienku, ze sucet dvoch ma byt parny, tak ma napadlo nieco taketo: je vytvarajuca fcia iba pre tie dva (zelena,modra)
je vytvarajuca fcia iba pre tie dva (zelena,modra)
t.j.  - a ak chces iba parne cleny, tak si mozes vsimnut, ze
- a ak chces iba parne cleny, tak si mozes vsimnut, ze
takze vytvarajuca funkcia co hladas bude
a hladas clen pri 
vychadza mi to 961 co je ine ako ↑ Jj:
Offline
#6 16. 06. 2014 17:42 — Editoval marketka01 (16. 06. 2014 18:23)
- marketka01
- Příspěvky: 26
- Reputace: 0
Re: PRIKLAD S KULICKAMA - Vytvorujici funkce, kombinatorika
↑ Brano:
Moc dekuju!!! A jeste bych se zeptala:
Nejde mi do hlavy, jak pri tomto soucinu rad: =tzn. soucin sude a liche
=tzn. soucin sude a liche
dostanu tohle:
???
Mam totiz dalsi priklad, kde potrebuju upravit tohle:
spis "intuitivne" jsem to upravila dle vzoru nahore takhle:
Je moje uvaha, prosim, spravna??
Dekuji!! :)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » PRIKLAD S KULICKAMA - Vytvorujici funkce, kombinatorika (TOTO TÉMA JE VYŘEŠENÉ)


 - to sa vola vynatie x pred zatvorku :-)
- to sa vola vynatie x pred zatvorku :-)
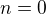 som to mal na mysli (co zodpoveda 0 cervenym a 61 moznosti ako vybrat zelene a modre)
som to mal na mysli (co zodpoveda 0 cervenym a 61 moznosti ako vybrat zelene a modre)