Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 11. 2014 14:29
- stuart clark

- Příspěvky: 1015
- Reputace: 7
inequality
Let  be positive real numbers such that
be positive real numbers such that  and
and 
Further, suppose that  and
and  Then how can we Prove that
Then how can we Prove that  and
and 
Offline
#3 15. 02. 2015 14:36
Re: inequality
↑ BakyX:
Nice solution. I need it for solving the problem of exponential equation.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 16. 02. 2015 23:06 — Editoval check_drummer (17. 02. 2015 00:05)
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: inequality
↑ BakyX:
Hi, at first sight (maybe i am wrong) there can be used "direct" solution, ie:
"Máte úhel beta." "No to nemám."
Offline


 are roots of
are roots of  and
and 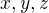 are roots of
are roots of  .
.
 and
and  since
since  and also
and also  and
and  since
since  . Also
. Also  ,
,  , so it must holds
, so it must holds  and
and  , so
, so  ,
,  and therefore
and therefore  .
. 

 , so q1=q2, so both polynomials are equal and so have the same roots.
, so q1=q2, so both polynomials are equal and so have the same roots.