Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 28. 04. 2009 15:46 — Editoval Rumburak (30. 04. 2009 10:00)
Re: Mocninné řady
Pro uvažované hodnoty proměnné x platí  (geom. řada o kvocientu x^9).
(geom. řada o kvocientu x^9).
Poloměr konvergence řady je 1, takže obě integrační meze leží uvnitř konvergenčního kruhu, tudíž na integračním intervalu řada konverguje stejnoměrně
a proto (též díky konečné délce tohoto intervalu) lze zaměnit pořadí sumy a integrace. Tedy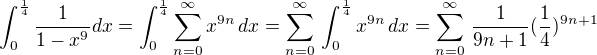 .
.
Odhadněme zbytek řady, k níž jsme došli: ,
, .
.
Číslo k zvolíme tak, aby  , a sečteme odpovídající počet členů příslušné řady. (Stačí vzít k=1).
, a sečteme odpovídající počet členů příslušné řady. (Stačí vzít k=1).
Poznámka: ... pokud jsem správně pochopil, co znamená "přesnost na 3 desetinná místa" - v tomto bodě si nejsem zcela jist. Kolik členů řady nutno sečíst , aby
přibližný desetinný rozvoj daného čísla se shodoval s jeho skutečným rozvojem až do 3. desetinného místa včetně, závisí nejen na přesnosti odhadu velikosti zbytku
řady, ale též na rozložení cifer ve skutečném (tj. nikloli jen přibližném) des. rozvoji daného čísla. Například zvýšíme-li číslo c = 1 999, 999 999 o hodnotu 10^(-6) ,
obdržíme 2 000 , takže chyba velikosti 10^(-6) se promítla do řádu tisíců.
Offline
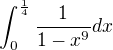 s přesností na 3 desetinná místa.
s přesností na 3 desetinná místa.