Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál - obecná platnost (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 12. 2007 20:34
Integrál - obecná platnost

Našel jsem tento vzoreček v tabulkách, ale jedna věc mě u toho zaráží.. Je pravda, že pokud přičtu k -ArcCotg(x) určitou konstantu, tak dostanu ArcTan(x), ovšem ta konstanta, kterou musím přičíst je, když se podívám na graf, v R+ je jiná než v R-. Znamená to, že ten vzorec platí, ale jen pokud se to rozdělí na intervaly (R+ a R-)? (teoreticky by pak mohly být nějaké problémy v určitých integrálech..)
Děkuju za odpověď
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#2 16. 12. 2007 21:45
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Integrál - obecná platnost
Nerozumím dotazu. Vzorec platí pro libovolné reálné x a na celém intervalu od minus nekonečna do nekonečna.
arctan x + acrcotg x=pi/2 tj C_1=C+pi/2
Offline
#3 16. 12. 2007 21:50
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Integrál - obecná platnost
První rovnítko je vzorce je v pořádku na celém r, funkci arctg(x)+C lze použít na počítání určitých integrálů bez problémů. Druhé rovnítko je v pořádku pouze na R+ a na R-, protože arccotg nemá v 0 derivaci. Pokud bys proto počítal určitý integrál pomocí druhého vzorce na intervalu [-a,b], musel bys ho spočítat zvláš? na intervalu [-a,0] a na [0,b] a výsledky sečíst (a a b jsou zde kladná čísla).
@robert.marik:bohužel ne, na kladných je to pi/2, na záproných -pi/2
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#4 16. 12. 2007 22:08
Re: Integrál - obecná platnost
@Kondr: Děkuju, zvedlo mi to náladu :-)
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#5 16. 12. 2007 23:47 — Editoval robert.marik (16. 12. 2007 23:51)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Integrál - obecná platnost
Hm, asi záleží na tom, jak se to bere. CAS Maple definuje arkuscontengens jako funkci inverzní k funkce cotangens na intervalu 0 až pi, potom je arkuscotangens v nule spojitý a má tam i derivaci a ten vzorec platí pro všechna R.
CAS Maxima definuje arkucotangens jako inverzni funkci k funkci contangens na intervalu -pi/2, pi/2. Potom to je tak jak pisou Saturday a Kondr.
NEvedel jsem ze jsou mozne oba pristupy, my jsme vzdycky pouzivali ten prvni. Tak jsem se ted divil, ale je to tak. Nemam po ruce treba Rektoryse abych se kouknul jak je to tam. Vlastne tu nemam zadnou knizku, ale aspon ten Maple dava za pravdu me, Maxima Saturdayovi a Kondrovi.
Odkaz http://mathworld.wolfram.com/InverseCotangent.html rozebira podrobne, ze jsou dve moznosti jak definovat arkuscotangens. Takze diky za upozorneni :)
Offline
#6 22. 06. 2009 14:44 — Editoval jelena (22. 06. 2009 14:59)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál - obecná platnost
Zdravím,
navazuji na téma a prosím o doplnění - jak má postupovat kolega, když dostane vyšetření takového průběhu funkce?:
http://forum.matweb.cz/viewtopic.php?pid=63008#p63008
viz debata, co se rozproudila v odkazovaném tématu. Děkuji :-)
Edit: Rektorys z roku 1973 má přesně to, co wikipedie, Bartsch z roku 1996 také a píše, že inverze se děla grafu goniometrických funkcí na intervalech, kde jsou ryze monotonni a které obsahuji počátek O.
Offline
#7 22. 06. 2009 16:19
Re: Integrál - obecná platnost
PlanetMath a Vojtěch Jarník se shodují na tom, že by to mělo být v 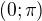 .
.
Zatím jediný, kdo tvrdí opak, je Wolfram (Mathematica) a Maxima.
Offline
#9 23. 06. 2009 00:31 — Editoval Olin (23. 06. 2009 00:32)
Re: Integrál - obecná platnost
Také zdravím :-)
Aby to ale nebylo tak jednoduché - jiná autorita, Abramowitz and Stegun, souhlasí prozměnu s Wolframem. Teda pokud jsem se správně zorientoval v tom mrňavém grafu se spoustou funkcí :-)
Offline
#10 23. 06. 2009 00:37 — Editoval jelena (23. 06. 2009 10:51)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál - obecná platnost
↑ Olin:
To jsem proluštila ještě z příspěvku ↑ robert.marik: - že jsou 2 názory a i v odkazovaném textu jsem to našla. Půjdu se podívat ještě na Východ - doplním:
také tak - spojitá verze pro obor hodnot od 0 do pi je vyznačena jako hlavní možná, pak jsou zakreslené pasy se spojitou hodnotou pro další periody.
Kniha z Odessy z roku 1910 o této problematice nepojednává (tomu bych ovšem věřila nejvíce).
Ještě toto: http://eom.springer.de/
------
editace: opravila jsem si pěknou hrubku ("z příspěvku", ne "s příspěvku" - čárky a háčky ve slovech - to už neovlivním, ale toto by byla hrůza)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál - obecná platnost (TOTO TÉMA JE VYŘEŠENÉ)