Matematické Fórum

↑ stenly:

Prosím - použij něco z odkazů, prostuduj tento materiál a konzultuj (pokud máš zájem), co se podařilo a co nejde - konkrétně.

Jinak to opravdu nepůjde.

Zdraví a děkuje Jelena

↑ Grimbor:

Zdravím a děkuji za příspěvek,

úprava není OK:



Více standardní úprava by bylo vytykání nejjvýšší mocniny (x^4), ale pro x k -oo není tak zřejmý výsledek ve znaménku, tak asi můžeš použit svůj postup po mé opravě.

OK?

↑ Grimbor:

Nevím, zda potřebuješ reakci na tento příspěvek, myslim, že problém chování funkce v -oo, +oo je už jasný.

Chyba tvé úpravy byla v tom, že nemůžeš jen tak škrtat v čitateli a v jmenovateli, pokud ten x není vtknut před závorku. Vykrátit jeden x ze součtu v jimenovateli je chyba z oblasti úpravy algebraických výrazu.

Platí, že pokud děliš minus minusem, tak vychazí plus.

Neděliš někonečně mnoho záporných prvku, ale polopaticky - nějaké záporné číslo hooooodně daleko nalevo od nuly.

OK?

↑ Grimbor:

Ahoj -),

   jen ke tvému dotazu.

Teď si něco vymyslím, nevztahuje se to konkrétně na tvůj příklad, ale aplikace je stejná.

Mám stac. body (podzření z extrémů): x=5; x=-2

Graficky se to ukáže asi nejjasněji:

-oo -------- -2 -------- 5 -------- +oo

Toto jsou mé intervaly monotonie, teď se chci podívat, kde má první derivace znaménko kladné/záporné (tím určím zda-li tam původní funkce roste/klesá (+/-)):

-oo -------- -2 -------- 5 -------- +oo
          +            -            +

   Když si k tomu nakreslíš šipky (nahoru - roste; dolu - klesá), tak to je ještě lépe vidět, ale ty já už tady nakreslit nějak pěkně a rozumě neumím, tak si je doplň sám.
   Logicky, když se na to podíváš s těmi šipkami, tak maximum může být jen tam, kde jde šipka zleva nahoru k bodu a vpravo dolu od bodu (tzn. do maxima funkce roste - nějak se tam musí dosta; z maxima funkce klesá - je to maximum, tak výše jít nemůže, tedy jediný směr už je dolu), obdobně u minima.

   Jinak můžeš potvrzovat extrémy pomocí druhé (a za určité podmínky další liché) derivace. Když bude druhá derivace kladná ve tvém stacionárním bodě (tj. funkce zde bude konvexní), pak je tento bod lokálním minimem. Analogicky pokud bude druhá derivace ve tvé mstacionárním bodě záporná (tj. funkce je zde konkávní) pak je tento bod lokální maximum. Znovu si to lze lehce představit:

   

   Z těhle "obrázků" (matici odpustí, jde jen o mnemotechnickou pomůcku) je vidět, že u 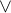můžeme říct něco jistě jen o jednom bodu a tím je ten úplně dole (logicky ho tedy nazvu minimem, pro naše potřeby tedy lokálním minimem), stejně tak můžeš říct jen o jednom jediném bodě u 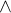něco jistě a to je, že bod úplně nahoře je nejvýše (logicky lokální maximum).
   Teď se zamyslíš a řekneš si, lokální maximum bude tehdy, když bude funkce ve stac. bodě (*) konkávní a to bude tehdy, bude-li tam druhá derivace záporná. Naopak minimum bude ve stac. bodě (*) tehdy, když v něm bude funkce konvexní a to je za předpokladu kladné druhé derivace.

* možná lepší říct okolo bodu včetně něj

Může ale vyjít druhá derivace rovna nule, pak nerozhodneš s pomocí druhé derivace, ale s pomocí další nenulové liché derivace (myslím, že liché, ale pro jistotu se podívej po netu, např. na wikipedii, atp..).

Snad pomůže taková mnemotechnická pomůcka, špatně se to ukazuje přes internet -)

PS: Obecně se tuším volí nějaká definice přes okolí, něco ve smyslu: pokud existuje nějaké okolí delat, kde je funkční hodnota f(x) na tomto okolí delta bodu A, kde bod A je stac. bod, menší/větší jak f(A), pak je v bodě A realizováno lok. maximum/minimum.

↑ O.o:
Ha! Dík za osvětlenou..  takže podle te první derivace je to v podstatě tak nějak jak jsem myslel ..  pokud mám u toho stacionárního bodu pomyslný "kopeček", tak je to maximum, naopak, pokud tam mám ďolíček, tak je to minimum ..hehe

No a podle te druhé derivace..koneckoncu to muže fungovat i jako taková "kontrola"  když porovnám konvexnost, konkavnost s maximem a minimem...aby to sedělo ...

Jen tedy, teď jsem opět narazil na takový problém, provedl jsem si určení inflexního budu + konvexity a konkavnosti.  Ale nějak tomu nerozumim ..
Když jsem si pročítal ten dokumet o průběhu funkce co je na Math-online...tak tam o inflexním bodu stojí:

Infexní bod je bod, pro který platí f''(x) = 0 a ve kterém se průběh funkce mění z konvexního nakonkávní, nebo naopak.

Mno.. určil sem si tedy inflexní bod tak že jsem položil druhou derivaci rovnou nule...ale když se koukám na tu tabulku, tak mi příjde že právě v tom inflexním bodě tj. v 0 ..se mi konvexnost, konkavnost nemění..mění se mi vlastně v jedničce  viz obrázek:

↑ O.o:
Vidíš, to jsem zcela přehlédl, že i u inflexních bodů se jedná pouze o podezření a že nemusí existovat..  Děkouji za osvětlenou!!

Mno..a ještě jsem si teda dodělal asymptoty ...s průběhem který mi vygeneroval mathweb mi víceméně souhlasí, ale přesto bych byl rád, kdybyste mi na ně koukli, odsouhlasili, popřípadě spřipomínkovali..

Překlepy a záludné chyby v elementárních úpravách, toť krutá daň za mnohé matematické večery a hektolitry vypité kávy ..hehe
Každopídně... děkuji mockamoc za pomoc při debugingu ...a pro pořádek tedy, zde posílám sofistikovanější upravenou verzi, ať jsou archívy úplné pro budoucí generace ...