Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 12. 2015 15:40 — Editoval liamlim (16. 12. 2015 18:22)
Něco jako kombinační čísla
Zdravím! Dokazováním něčeho jsem došel k zajímavému poznatku, který neumím dokázat. Pokud to někdo umí, pak prosím o návod, protože by mě to zajímalo. Všimněte si, že:










Pro 13 už to psát nebudu, ale taky jsou všechny  kromě
kromě  dělitelné 13. Může mi někdo poradit, jak by to šlo dokázat? Nezdá se mi to jako náhoda...
dělitelné 13. Může mi někdo poradit, jak by to šlo dokázat? Nezdá se mi to jako náhoda...
Jinak, snadno se dokáže, že:  ,
, 
Asi by pomohlo najít nějaký vzorec, ale nejsem toho schopen. Jinak... Na závěr uvedu, jak mě napadlo dělat podobné věci. Jednoduše jsem si hrál s velkou fermatovou větou. Tedy:
Pro libovolné  platí
platí  což se dokáže snadno indukcí. Potom pro prvočíselné
což se dokáže snadno indukcí. Potom pro prvočíselné  a
a 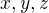 nesoudělná lze docela snadno odvodit následující:
nesoudělná lze docela snadno odvodit následující:
1)  nedělí
nedělí  . / asi chybne/
. / asi chybne/
2) Existují nesoudělná  ,
,  taková, že
taková, že  ,
,  ,
,  ,
,  ,
,  ,
, 
(pozn. první je třeba dokázat (2) a z toho odvodit (1))
To vše jenom abych ukázal, že podle mě uvedené rozklady mají docela smysl. Pro důkazz (1) a (2) je potřeba jen hodnota  , ale stejně by mě docela zajímaly ostatní. Za jakékoliv nápady bych byl vděčný!
, ale stejně by mě docela zajímaly ostatní. Za jakékoliv nápady bych byl vděčný!
Offline
#2 03. 12. 2015 17:24
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Něco jako kombinační čísla
↑ liamlim:
Ahoj,
1) je to opravdu tak, že n nedělí xyz? Mám pocit, že při důkazu VFV (alespoň pro regulární prvočísla) se právě rozlišují případy "n dělí" a "n nedělí". Můžeš prosím dokázat 2 a 1 detailněji?
2) Co znamená index z u  ? - tedy není jedno a, ale tři (pro x,y a z)?
? - tedy není jedno a, ale tři (pro x,y a z)?
3) Píšeš, že  , ale o kus výše vidím f(3,1)=-3, tak ja to tedy je?
, ale o kus výše vidím f(3,1)=-3, tak ja to tedy je?
4) Aby bylo možné  využít, je nutné určit hodnotu f(n,0) pro libovolné n.
využít, je nutné určit hodnotu f(n,0) pro libovolné n.
"Máte úhel beta." "No to nemám."
Offline
#3 03. 12. 2015 17:46 — Editoval liamlim (03. 12. 2015 17:50)
Re: Něco jako kombinační čísla
↑ check_drummer:
(1) Rozepíši
(2) To je nějaké celé číslo. Ta rovnost  spolu s
spolu s  znamená, že pokud existují
znamená, že pokud existují  ,
,  ,
,  pro které věta platí, pak existují také
pro které věta platí, pak existují také  ,
,  celá. Analogicky
celá. Analogicky  , atd.
, atd.
(3) chyba. má být  . Opravím.
. Opravím.
(4) Dodefinujme  pokud
pokud  nebo
nebo 
Offline
#4 03. 12. 2015 17:48
Re: Něco jako kombinační čísla
↑ liamlim:
Pokud správně chápu konstrukci čísel  , tak dle Tvého značení platí
, tak dle Tvého značení platí
kde  jsou nějaká celá čísla. Matematickou indukcí lze z tohoto a ze skutečnosti, že binomické koeficienty
jsou nějaká celá čísla. Matematickou indukcí lze z tohoto a ze skutečnosti, že binomické koeficienty 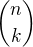 jsou vždy dělitelné číslem
jsou vždy dělitelné číslem  pro
pro  , je-li
, je-li  je prvočíslo, odvodit tu dělitelnost 5, 7, 13 apod. Všimni si, u 4 a u ostatních složených čísel dělitelnost platit nebude.
je prvočíslo, odvodit tu dělitelnost 5, 7, 13 apod. Všimni si, u 4 a u ostatních složených čísel dělitelnost platit nebude.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#5 03. 12. 2015 17:53
Re: Něco jako kombinační čísla
↑ Pavel:
Díky! To vypadá dobře. Zkusím nad tím ještě popřemýšlet.
↑ check_drummer:
Nejradši bych rád viděl, jestli se nenajde chyba v něčem, co jsem dosud napsal. Protože ten důkaz je takový psavý. Ale určitě ho napíši.
Offline
#6 03. 12. 2015 18:07 — Editoval liamlim (03. 12. 2015 18:55)
Re: Něco jako kombinační čísla
Důkaz části 2:
1. krok Označme nejvyšší společný dělitel čísel  ,
, 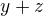 jako
jako  . Potom pro nějaká celá
. Potom pro nějaká celá 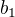 ,
, 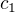 nesoudělná platí
nesoudělná platí  ,
,  . Zřejmě
. Zřejmě  dělí
dělí  , jak plyne z
, jak plyne z  . Odsud - vzhledem k nesoudělnosti
. Odsud - vzhledem k nesoudělnosti 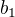 ,
, 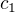 plyne, že
plyne, že 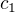 dělí
dělí  .
.
2. krok Označme nejvyšší společný dělitel čísel  ,
, 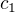 jako
jako 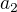 . Potom pro nějaká nesoudělná
. Potom pro nějaká nesoudělná  ,
,  platí
platí 

A platí, že  dělí
dělí  neboli
neboli  dělí
dělí  .
.
...
k-tý krok: Označme nejvyšší společný dělitel čísel 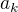 ,
, 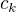 jako
jako  . Potom pro nějaká nesoudělná
. Potom pro nějaká nesoudělná  ,
,  platí
platí 

A platí, že  dělí
dělí  neboli
neboli  dělí
dělí  .
.
....
(n-1)-tý krok: Označme nejvyšší společný dělitel čísel  ,
,  jako
jako 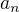 . Potom pro nějaká nesoudělná
. Potom pro nějaká nesoudělná  ,
,  platí
platí 

A platí, že  dělí
dělí  neboli
neboli  dělí
dělí  .
.
Odsud máme  .
.
Tak, teď se podíváme, čemu se vlastně rovnají  a
a 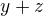 . Máme:
. Máme:

Pokud není někde chyba v myšlence, pak bych teď rád ukázal, že součin 
Nyní upravujeme:

Tak, skoro hotovo. Teď stačí dosadit již spočítané hodnoty a dojít k tomu, že se rovnost vydělí  . Pak se stačí podívat se na nejmenší mocniny u všech výrazů v součtu a celou rovnost vydělit. Po tomto vydělení ve všech závorkách kromě té u
. Pak se stačí podívat se na nejmenší mocniny u všech výrazů v součtu a celou rovnost vydělit. Po tomto vydělení ve všech závorkách kromě té u  vyjde alespoň druhá mocnina u
vyjde alespoň druhá mocnina u  . Přitom
. Přitom  , což druhá mocnina není. Odsud plyne, že
, což druhá mocnina není. Odsud plyne, že 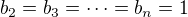 .
.
Po dosazení hned máme 
 .
.
Tedy ukázal jsem, v jakém tvaru jsou  a
a 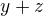 .
.
Uf, snad jsem to dopsal. Samozřejmě je možné, že jsem někde něco přehlédl nebo něco úplně přesně neplatí. No nakonec kvůli tomuto "důkazu" jsem sem původně nepsal, protože mě jen zajímalo to s těmi prvočísly.
Offline
#7 03. 12. 2015 22:55
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Něco jako kombinační čísla
↑ liamlim:
Jak jsi prosím odvodil  ?
?
Stále jsi neurčil f(n,0).
v posledním příspěvku - tvá úvaha dlé mého selže, pokud bude některé  .
.
"Máte úhel beta." "No to nemám."
Offline
#8 03. 12. 2015 23:14 — Editoval liamlim (03. 12. 2015 23:16)
Re: Něco jako kombinační čísla
↑ check_drummer:
Tedy odvození:
To vynásobím (x+y) a dostanu: (teď budu místo 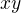 psát 1. Tím nepřijdu o žádnou informaci, rovnost bude poté stačit zhomogenizovat (alespoň tuším že se tomu tak říká)
psát 1. Tím nepřijdu o žádnou informaci, rovnost bude poté stačit zhomogenizovat (alespoň tuším že se tomu tak říká)
Odsud
Teď to převedu na jednu sumu. Aby byl převod jednodušší, zavedu si 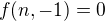 a
a  . S tímto již mohu beztrestně provézt:
. S tímto již mohu beztrestně provézt: 
Odsud ale již přímo plyne  což po dosazení n namísto n+1 dává dokazované.
což po dosazení n namísto n+1 dává dokazované.
Pozn. Hodnoty  lze taky odvodit pouze z toho vzatahu. Pokud namísto všech "divných" členů dosadíme 0. Vychází takto: 0 pro liché n, 2 pro dělitelné 4 a -2 pro ostatní
lze taky odvodit pouze z toho vzatahu. Pokud namísto všech "divných" členů dosadíme 0. Vychází takto: 0 pro liché n, 2 pro dělitelné 4 a -2 pro ostatní
Offline
#9 03. 12. 2015 23:30 — Editoval liamlim (03. 12. 2015 23:31)
Re: Něco jako kombinační čísla
Všiml jsem si nové věci. Pro prvočíselná  platí, že součet všech
platí, že součet všech  je roven 1. Alespoň pro všechna do n = 13. Dále jsem to ručně nezvládl počítat. To mi přijde fascinující. Nemáte nápad, jak to dokázat?
je roven 1. Alespoň pro všechna do n = 13. Dále jsem to ručně nezvládl počítat. To mi přijde fascinující. Nemáte nápad, jak to dokázat?
Offline
#10 03. 12. 2015 23:47 — Editoval Pavel (04. 12. 2015 21:09)
Re: Něco jako kombinační čísla
Prostřednictvím derivací lze ukázat, že pro 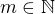 platí
platí![kopírovat do textarea $
f(2m,0)&=(-1)^m\cdot 2\\[.5\baselineskip]
f(2m,2)&=-\frac 1{1!}\cdot\left[\frac{t^2}{t^2-1}\cdot\frac{\mathrm d}{\mathrm d t}\left(t^m+t^{-m}\right)\right]_{t=-1}=(-1)^{m+1}\cdot m^2\\[.5\baselineskip]
f(2m,4)&=\frac 1{2!}\cdot\left[\frac{t^2}{t^2-1}\cdot\frac{\mathrm d}{\mathrm d t}\left(\frac{t^2}{t^2-1}\cdot\frac{\mathrm d}{\mathrm d t}\left(t^m+t^{-m}\right)\right)\right]_{t=-1}=(-1)^{m+2}\cdot m\sum_{i=0}^{\lceil\frac m2\rceil-1}(m-1-2i)^2\\[.5\baselineskip]
f(2m,6)&=-\frac 1{3!}\cdot\left[\frac{t^2}{t^2-1}\cdot\frac{\mathrm d}{\mathrm d t}\left(\frac{t^2}{t^2-1}\cdot\frac{\mathrm d}{\mathrm d t}\left(\frac{t^2}{t^2-1}\cdot\frac{\mathrm d}{\mathrm d t}\left(t^m+t^{-m}\right)\right)\right)\right]_{t=-1}\\[.5\baselineskip]
&\vdots\\[.5\baselineskip]
f(2m,2k)&=\frac{(-1)^k}{k!}\cdot\left[\left(\frac{t^2}{t^2-1}\cdot\frac{\mathrm d}{\mathrm dx}\right)^k(t^m+t^{-m})\right]_{t=-1},\qquad 0\leq k\leq m
$](/mathtex/7e/7e53568bfd7c1fe6a04961fbf33953c0.gif)
Člen  lze vyjádřit také bez diferenciálního operátoru jako k-1 do sebe vnořených sum a součinů. Zápis je však poněkud komplikovanější.
lze vyjádřit také bez diferenciálního operátoru jako k-1 do sebe vnořených sum a součinů. Zápis je však poněkud komplikovanější.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#11 04. 12. 2015 01:17
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Něco jako kombinační čísla
↑ liamlim:
Ahoj, napadl mě důkaz vskutku geniální (a to se nerad chválím - asi už je pozdě):
Volme jako x,y (komplexní) čísla splňující x.y=1 a x+y=1 - a potom se tvé vztahy velmi zjednoduší na  , kde c je součet koeficientů f(p,i). Chceme dokázat, že c=0 - tedy jinými slovy, že
, kde c je součet koeficientů f(p,i). Chceme dokázat, že c=0 - tedy jinými slovy, že  . Ovšem
. Ovšem  , tj. x,y tvoří vrcholy pravidleného šestiúhelníka. A protože (teď to přijde) každé prvočíslo
, tj. x,y tvoří vrcholy pravidleného šestiúhelníka. A protože (teď to přijde) každé prvočíslo  je tvaru
je tvaru  , tak bude
, tak bude  - a tedy
- a tedy  (protože x+y=1). Skvělé, že? Asi z toho neusnu. :-)
(protože x+y=1). Skvělé, že? Asi z toho neusnu. :-)
"Máte úhel beta." "No to nemám."
Offline
#12 04. 12. 2015 21:48 — Editoval Pavel (04. 12. 2015 21:49)
Re: Něco jako kombinační čísla
Pro úplnost uvádím vyjádření koeficientů  pro sudé argumenty prostřednictvím sum:
pro sudé argumenty prostřednictvím sum:![kopírovat do textarea $
f(2n,0)&=(-1)^n\cdot 2\\[.5\baselineskip]
f(2n,2)&=(-1)^{n+1}\cdot n^2\\[.5\baselineskip]
f(2n,4)&=\frac{(-1)^{n+2}}{2}\sum_{i=0}^{\lceil\frac n2\rceil-1}n(n-1-2i)^2\\[.5\baselineskip]
f(2n,6)&=\frac{(-1)^{n+3}}{6}\sum_{i_1=0}^{\lceil\frac n2\rceil-1}\sum_{i_2=0}^{\lceil\frac{n-1}2-i_1\rceil-1}n(n-1-2i_1)(n-2-2i_1-2i_2)^2\\[.5\baselineskip]
f(2n,8)&=\frac{(-1)^{n+4}}{24}\sum_{i_1=0}^{\lceil\frac n2\rceil-1}\sum_{i_2=0}^{\lceil\frac{n-1}2-i_1\rceil-1}\sum_{i_3=0}^{\lceil\frac{n-2}2-i_1-i_2\rceil-1}n(n-1-2i_1)(n-2-2i_1-2i_2)(n-3-2i_1-2i_2-2i_3)^2\\[.5\baselineskip]
&\vdots\\[.5\baselineskip]
f(2n,2k)&=\frac{(-1)^{n+k}}{k!}\sum_{i_1=0}^{\lceil\frac n2\rceil-1}\sum_{i_2=0}^{\lceil\frac{n-1}2-i_1\rceil-1}\sum_{i_3=0}^{\lceil\frac{n-2}2-i_1-i_2\rceil-1}\cdots\sum_{i_{k-1}=0}^{\lceil\frac{n-k+2}2-\sum_{j=1}^{k-2}i_j\rceil-1}\left(n-k+1-2\sum_{j=1}^{k-1}i_j\right)\times\\
&\quad\times\prod_{s=0}^{k-1}\left(n-s-2\sum_{j=1}^si_j\right)
$](/mathtex/3b/3b194f909ea4ff4a78455075c7364bb2.gif)
kde  .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#13 04. 12. 2015 21:57 — Editoval liamlim (04. 12. 2015 22:29)
Re: Něco jako kombinační čísla
↑ Pavel:
To je až tak úžasné, že si neumím představit odvození tohoto. Ale když už jsme u toho vyjádření sudých...
Pak platí následující:
Tedy 
Neboli
platí dokonce:
pozn: zase jsem pro přehlednost vypustil 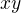 které lze snadno doplnit.
které lze snadno doplnit.
Snadno lze rozmyslet, že po roznásobení závorky na pravé straně vlastně dostaneme hledaný tvar. Tedy podle mého názoru by se nejvíc hodilo nalézt nějaké vyjádření pro lichá... Ale i tak, neuvěřitelné, že lze něco podobného odvodit.
Offline
#14 04. 12. 2015 22:02
Re: Něco jako kombinační čísla
Pozn. Všiml jsem si dalšího zajímavého faktu:
Důkaz tohoto by měl být lehčí. Vztah píší tak trochu pro zajímavost.
Jen tak mimochodem - neznáte někdo nějaký text o těchto číslech? v matice se napsalo už o všem a zrovna o těchto podivných číslech bych se rád dozvěděl víc.
Offline
#15 04. 12. 2015 23:58
Re: Něco jako kombinační čísla
↑ liamlim:
Koeficienty pro liché argumenty se mi zdály právě těžší. Jinak zde je zřejmě to, co hledáš. Ty koeficienty tomu nasvědčují.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#16 05. 12. 2015 00:13 — Editoval liamlim (05. 12. 2015 00:53)
Re: Něco jako kombinační čísla
↑ Pavel:
Díky. Jsem rád, že konečně vím, že se těm číslům říká Lucasova čísla. Je to vážně zajímavé. Už jen třeba ta souvislost s fibonacciho čísly...
Teď jsem přemýšlel taky nad další věcí. Zabýval jsem se vyjádřením součtu  . Vlastně jsem vyjadřoval tuto hodnotu za pomoci
. Vlastně jsem vyjadřoval tuto hodnotu za pomoci  ,
,  . Napadlo mě.. Co takhle zkusit vyjádřit
. Napadlo mě.. Co takhle zkusit vyjádřit podle
podle  ,
,  ,
,  . Je jasné, že platí:
. Je jasné, že platí:
Pokud označím  pak mám vyjádření posloupnosti rekurentně... Stačí doplnit
pak mám vyjádření posloupnosti rekurentně... Stačí doplnit  ,
, 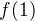 ,
,  .
.
Neznám generující funkce, ale myslím, že za pomoci toho se odvozovaly vzorce pro  právě u podobných posloupností, ne? Nešlo by to i tady?
právě u podobných posloupností, ne? Nešlo by to i tady?
Z toho mnou napsaného vyjádření taky jde snadno vidět, že libovolný výraz tvaru  lze zapsat jako součet nějakých součinů
lze zapsat jako součet nějakých součinů  ,
,  ,
,  . Bohužel neumím přesně vyjádřit jakých. Ale toto mě vše baví.. Přemýšlet nad tím jen tak nepřestanu
. Bohužel neumím přesně vyjádřit jakých. Ale toto mě vše baví.. Přemýšlet nad tím jen tak nepřestanu

...
Tedy má hypotéza je, že zase mají koeficienty co dělat s prvočísly :D někdo na dokázání?
Offline
#17 05. 12. 2015 18:45 — Editoval check_drummer (05. 12. 2015 18:45)
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Něco jako kombinační čísla
liamlim napsal(a):
Ahoj, nechybí ti tam činitelé  ?
?
"Máte úhel beta." "No to nemám."
Offline
#18 05. 12. 2015 18:46
Re: Něco jako kombinační čísla
↑ check_drummer:
chybí. Ale ti jdou snadno doplnit tak, aby součet mocnin odpovídal. Řekněme, že jsem zvolil 
Offline
#19 05. 12. 2015 18:49
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Něco jako kombinační čísla
↑ liamlim:
Já jen jestli mají ty koefieinty f stále stejný význam... Takže mají.
"Máte úhel beta." "No to nemám."
Offline
#20 05. 12. 2015 18:51
Re: Něco jako kombinační čísla
↑ check_drummer:
Jak tam pracuji už s tím A, B, C, tak už ne! Tam jsem velmi nešťastně zvolil pro funkci stejný název, tedy f.
Offline
#21 05. 12. 2015 23:19
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Něco jako kombinační čísla
↑ liamlim:
Mohl bys sem prosím napsat vyjádření f i pro další hodnoty? nejen pro f(2) a f(7)? Lépe by se mi to pak zkoumalo.
"Máte úhel beta." "No to nemám."
Offline
#22 05. 12. 2015 23:33 — Editoval liamlim (05. 12. 2015 23:38)
Re: Něco jako kombinační čísla
↑ check_drummer:
Něco ještě lepšího. Zkusím dát návod, jak se to dělá. Vytvořit poté program, který vyjádření vytvoří by poté nemělo být těžké.


Toto jsou základní členy, ze kterých odvodíme všechny následující. Abychom spočítali  pak vynásobíme
pak vynásobíme  číslem
číslem  ,
, 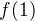 číslem
číslem  ,
,  číslem
číslem  . A sečteme. Tedy:
. A sečteme. Tedy:

atd.
Já ale počítám ty hodnoty trochu jinak. Ono když položíme  (o žádnou informaci nepřijdeme. Zpětně stačí dosadit mocniny
(o žádnou informaci nepřijdeme. Zpětně stačí dosadit mocniny  tak, aby součet odpovídal. S tím, že
tak, aby součet odpovídal. S tím, že  je za dvě
je za dvě  a
a  je za tři
je za tři  .) Pak máme:
.) Pak máme:
Pravidlo se pro výpočet bez počítače zrychlí, protože nenásobíme jeden řádek, ale jen přičítáme.







Offline
#23 05. 12. 2015 23:51 — Editoval liamlim (05. 12. 2015 23:53)
Re: Něco jako kombinační čísla
mimochodem, odtud jde odvodit taky zajímavé věci. Volbou  totiž získáme například, že
totiž získáme například, že
Pokud  pak
pak
Zase mám takové myšlenky zkusit dosadit místo  ,
,  ,
,  nějaké
nějaké  té mocniny a zkusit něco zajímavého odvodit ale radši ne. Nad velkou fermatovou větou už jsem strávil dost času.
té mocniny a zkusit něco zajímavého odvodit ale radši ne. Nad velkou fermatovou větou už jsem strávil dost času.
Offline
#24 24. 12. 2015 14:26 — Editoval liamlim (24. 12. 2015 14:56)
Re: Něco jako kombinační čísla
Dnes jsem si odvodil další zajímavý fakt ohledně součtů. Platí:
Jestliže  pak pro přirozené liché
pak pro přirozené liché  platí:
platí:
Důkaz je snadný, ale odvození snadné nebylo :D Chtěl jsem nějaký pěkný vztah, ve kterém budu mít vyjádřeny součty. Ono totiž z tohoto snadno odvodíme, že pro libovolná  platí
platí
S tím, že teď už mám jen výrazy ve tvaru  nebo
nebo  . a ty jsem schopen nahradit za pomoci čísel
. a ty jsem schopen nahradit za pomoci čísel  . No toto ještě zkusím. Když už mám konečně ty prázdniny a můžu si odvozovat co mě baví.
. No toto ještě zkusím. Když už mám konečně ty prázdniny a můžu si odvozovat co mě baví.
EDIT: Označme  pro
pro  . Pak označme též
. Pak označme též

Pak snadno nahlédneme, že:


Ostatní už odvodíme z těchto:


atd.
Obecně  což je snadné ukázat.
což je snadné ukázat.
Teď nějak přijít na to, jak obecně vyjádřit  a dostaneme něco zajímavého.
a dostaneme něco zajímavého.
Offline
#25 26. 12. 2015 00:24
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Něco jako kombinační čísla
liamlim napsal(a):
Obecně
Ahoj, zkus hledat hesla "diferenční rovnice" a/nebo hledat 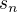 ve tvaru
ve tvaru 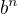 , resp. ve tvaru lineární kombinace dvou takových vyjádření.
, resp. ve tvaru lineární kombinace dvou takových vyjádření.
"Máte úhel beta." "No to nemám."
Offline
