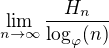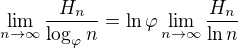Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 09. 03. 2016 22:51 — Editoval Freedy (09. 03. 2016 22:54)
Re: Limitny maraton
↑↑ Marian:
Abych pravdu řekl, ať jsem dáte jakoukoliv limitu (až na nějaké pikantnosti), tak se určitě na nějakém fóru někdy řešila. Proto mi přijde trapné (nedůstojné), že radši hledáte, zda-li se nějaká podobná limita řešila někde jinde, namísto toho, abyste se ji sami pokusili vyřešit. Já řeším limity tak, že ji zkusím sám spočítat, né tak, že bych je vermo mocí hledal na internetu.
Toť můj názor, doufám že tím nikoho neurazím.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#27 10. 03. 2016 07:13 — Editoval Marian (11. 03. 2016 19:07)
Re: Limitny maraton
Offline
#28 10. 03. 2016 12:52
Re: Limitny maraton
Pozdravujem ↑ Marian:,
Dakujem o tvoj zaujem o toto vlakno.
Zda sa mi, ze Tvoj odkaz je zaujimavy a moze poucit citatelov vlakna. A co je iste ze ak niekto da ine riesenie, to nebude kopia tvojho zaujimaveho vlakna.
Tak sa mi zda, ze skryt Tvoj odkaz by bola skoda.
Iste Freedy nam prida aj jeho riesenie, ako "autor" cvicenia.
Je trochu skoda, ze na takomto vlakne nevidime dost studentov, vsak to by mohlo idealne byt ich vlakno, kde by mohli dat ich skusenosti z ich skusok...
Dobre pokracovanie vo tvojej praci.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#29 11. 03. 2016 10:57
Re: Limitny maraton
Cvicenie 8
Mala pomoc.
Mozte zacat pracovat na  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#30 11. 03. 2016 12:35
Re: Limitny maraton
Cvičení 8
Malá pomoc II
Limitu lze vyřešit na jednom řádku. Lze ukázat, že se nejedná o nic jiného než o definiční vztah druhé derivace funkce  v bodě
v bodě  .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#31 11. 03. 2016 20:53
Re: Limitny maraton
Ahoj ↑ Pavel:, mas pravdu, ze viac moznosti na vysetrenie danej limity.
Napr. Pouzitie rozvojov v okoly nekonecna je dalsia metoda.
Ak nikdo neda riesenia v dohladnej dobe, tak navrhujem aby sme ty a ja dali po tyzdny nase riesenia. ( studentom to moze byt uzitocne)
Pevny week-end.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#32 21. 03. 2016 18:10 — Editoval vanok (21. 03. 2016 18:11)
Re: Limitny maraton
Cvicenie 8
Ako som slubil, davam tu jedno elementarne riesenie tomto cvicenia.
Poznamka, predpokladam ze x>0 pre vsetky upravy.
Tu sa mozu pouzit konjugovane vyrazy kazdej zatvorky:v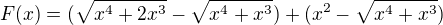
A dostaneme 
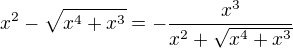
Cize 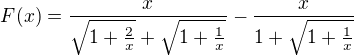
Po vyjadreni na spolocneho menovatela 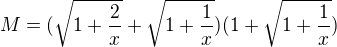
Dostaneme citatel  ktoreho konjugovany vyraz je
ktoreho konjugovany vyraz je 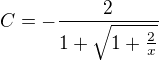
A na koniec konstatujeme, ze hladana limita je 
Dufam, ze ini ucastnici odpovedia, na neukoncene riesenia cviceni, v duchu tohto vlakna, za co im vopred dakujem ( ako aj students, ktorim cakane riesenia mozu posluzit).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#34 22. 03. 2016 23:48 — Editoval vanok (23. 03. 2016 03:55)
Re: Limitny maraton
Pridam hned dalsie cvicenie, ake mozme casto vidiet na skuskach.
( dufam ze aj kolega ↑ Pavel: prida jeho. Tiez podla duchu tohto vlakna, kolega Freedy by mal dat jeho riesenie problemu, ktory navrhol a dat dalsie cvicenie zo skusok. )
cvicenie 9
Najdite limitu postupnosti ![kopírovat do textarea $a_n=\frac 1n \sqrt [n]{\prod_{k=1}^n{(n+k)}}$](/mathtex/0d/0df9584d612cfde77a262d9afff0cd6d.gif) v
v  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#35 24. 03. 2016 22:29 — Editoval Freedy (25. 03. 2016 13:17)
Re: Limitny maraton
Ahoj,
řešení cvičení 9
Cvičení 10
Nechť
 značí i-té prvočíslo a
značí i-té prvočíslo a 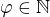 pevné.
pevné.Označme
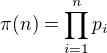

Určete následující limitu:
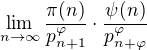
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#36 25. 03. 2016 19:33 — Editoval vanok (25. 03. 2016 23:39)
Re: Limitny maraton
Ahoj ↑ Freedy:,
cvicenie 9,
Sa da riesit aj takto.
Vyhodaje, ze netreba ani poznat Stirling-ov vzorec.
Pripominam ti, ze cakane na tvoje riesenie cvicenia 7.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#37 26. 03. 2016 17:30 — Editoval Freedy (26. 03. 2016 17:32)
#38 27. 03. 2016 10:17
Re: Limitny maraton
↑ Freedy:,
Ahoj,
Ked si uz davas cvicenia zo skusok, tak nie je zbytocne dat aj tvoje studenstke riesenie. To by sa iste pacilo tvojim kolegom.
Vsak casto je viac moznosti na ich riesenie...
Tiez, pripominam, ze ak ma byt toto vlakno dynamicke je dobre aby ich autor, ak ich nikto neriesil,dal "maly navod" k ich rieseniu a po takom tyzdni ( bez reakcii) dal jeho autorske riesenie.
Na viac, moze byt uzitocne, po rieseni foristami, ze autor prida este doplnujuce riesenie, ktore moze byt uzitocne kolegom.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#41 03. 04. 2016 23:03
Re: Limitny maraton
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#42 05. 04. 2016 13:20 — Editoval vanok (05. 04. 2016 13:22)
Re: Limitny maraton
Ahoj ↑ Freedy:,
Zaujimave krake cvicenie, ktore sa najde asi v kazdej prednaske z analyzy.( v prvom rocniku ?)
Osobne by som pridal okamzite po jeho vyrieseni (a. équivalentna z
équivalentna z  v + nenonecne) dve otazky.
v + nenonecne) dve otazky.
b. Ukazte, ze 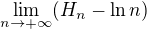 existuje ( Euler-ova konstatanta), oznacme ju
existuje ( Euler-ova konstatanta), oznacme ju 
c.Ukazte, ze v okoli  mame
mame 
Cize ist, vdaka dalsim otazkam na skuske tak daleko, ako je schopny dobry student...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#43 08. 04. 2016 19:28
Re: Limitny maraton
Cvicenie 11 a doplnky.
Navod.
Co sa tyka otazky a. je mozne pouzit, ze
funkcia  pre t>0 je klesajuca a:
pre t>0 je klesajuca a:![kopírovat do textarea $\forall k \ge 1\forall t \in [k;k+1],\frac 1{k+1} \le \frac 1t \le \frac 1 k$](/mathtex/2b/2b462b72b7eed997ef05296f8750e1a6.gif)
integraciou nerovnosti na ![kopírovat do textarea $ [k;k+1]$](/mathtex/43/4383a2b3fe5453e584739cc642a0d8b7.gif) nerovnosti ktorych sumacia da riesenie cvicenia a. ( ako aj podstatnu cast povodneho cvicenia a.)
nerovnosti ktorych sumacia da riesenie cvicenia a. ( ako aj podstatnu cast povodneho cvicenia a.)
Co sa tyka otazky b., moze sa pouzit najdena nerovnost v casti a.
Riesenie otazky c. sa moze zacat vysetrenim postupnosti 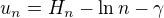
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#44 11. 04. 2016 18:56 — Editoval vanok (21. 04. 2016 22:36)
Re: Limitny maraton
cvicenie 11, pokracovanie (otazka a.)![kopírovat do textarea $\forall k \ge 1\forall t \in [k;k+1],\frac 1{k+1} \le \frac 1t \le \frac 1 k$](/mathtex/2b/2b462b72b7eed997ef05296f8750e1a6.gif)
nam po integracii da![kopírovat do textarea $\forall k \ge 1\forall t \in [k;k+1],\frac 1{k+1} \le \int_{k}^{k+1}\frac 1tdt=\ln (k+1)-\ln (k) \le \frac 1 k$](/mathtex/a3/a34a93196bb53aecf91ac732182d370e.gif)
co po sumacii od 1 do n-1 da
a z toho
A tak 
co znamena tiez 
(odpoved na povodnu otazku cvicenia 11, od kolegu Freedy dostaneme okamzite vdaka vzorcu zmeny bazy logaritmu )
Na ostatne 2 otazky necham este trochu casu kolegom co maju chut napisat ich riesenie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#45 18. 04. 2016 02:17
Re: Limitny maraton
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#46 21. 04. 2016 22:36 — Editoval vanok (22. 04. 2016 02:32)
Re: Limitny maraton
Cvicenie 11,
Ano pekne si doplnil to riesenie.
Mozno by bolo zaujimave vediet ake otazky ti mohol polozit skusajuci po (pri) jeho rieseni.
Neviem na ktorych VS v cz, sk sa uci Stolz-ova veta alebo aspon verziu povodnej Cesàrov-over vety.
Mozte ma poucit.
Cvicenie 12
a. = aj cvicenie 11.
b.
Tu je mozne vyuzit riesenie otazky a.
Presnejsie mame pre  , ze
, ze 
Ale ohranicenie z a. da aj 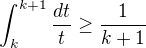
a preto 
Tak rada vseobecneho clenu 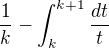 konverguje (Lebo jej cleny su kladne a mensie ako vseobecny clen jednej konvergentnej rady.)
konverguje (Lebo jej cleny su kladne a mensie ako vseobecny clen jednej konvergentnej rady.)
Co znamena, ze sucet postupnosti vseobecneho clenu  konverguje k
konverguje k  , co ukoncuje dokaz otazky b.
, co ukoncuje dokaz otazky b.
c. Iste to chce niekto skusit...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#47 15. 05. 2016 17:50
Re: Limitny maraton
c. Navod
Clen z 
Preto moze byt zaujimave vysetrit postupnost vseovecneho clenu 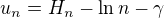
( mozte nast ekvivalent postupnosti  )
)
Podobne mozte vysetrit aj clen z  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#48 24. 05. 2016 00:00
Re: Limitny maraton
Cvicenie 13
Nech 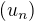 je jedna postupnost taka, ze
je jedna postupnost taka, ze ![kopírovat do textarea $ u_0 \in ]0;\frac{\pi}2]$](/mathtex/74/74812c4b7aae37f72faef0a3f049fe97.gif) a
a  pre kazde prirodzene n.
pre kazde prirodzene n.
a)Dokazte ze 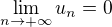 a najdite ekvivalent
a najdite ekvivalent  v
v 
b)Najdite dvojclenny asymptoticky rozvoj  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#49 12. 06. 2016 15:31
Re: Limitny maraton
Cvicenie 13,
Myslienky na zaciatok riesenia.
Akoze tu ide o postupnost typu  , tak vieme, ze ak taka postupnost konverguje tak jej limita je pevny bod funkcie
, tak vieme, ze ak taka postupnost konverguje tak jej limita je pevny bod funkcie 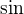
Tak je uzitocne dokazat, ze 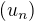 je monotonna a ohranicena
je monotonna a ohranicena
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#50 27. 01. 2017 22:43
Re: Limitny maraton
Cvicenie 13, cake na riesenie.
Cvicenie 14
Ako by ste ( co najucinnejie ) nasli 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

![kopírovat do textarea $
\lim_{x\to\infty}\left(\sqrt{x^4+2x^3}+x^2-2\sqrt{x^4+x^3}\right)
&=\lim_{x\to\infty}\frac{\sqrt{1+\frac 2x}-2\sqrt{1+\frac 1x}+1}{\frac 1{x^2}}
=\lim_{h\to 0^+}\frac{\sqrt{1+2h}-2\sqrt{1+h}+1}{h^2}\\[.5\baselineskip]
&=\left.\left(\sqrt{1+x}\right)''_+\right|_{x=0}
=\left.-\frac 1{4\sqrt{(1+x)^3}}\right|_{x=0}=-\frac 14\,.
$](/mathtex/94/947ecdd72d54e17fac1242887e965952.gif)
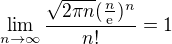
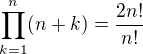
![kopírovat do textarea $Q = \lim_{n\to\infty }\frac{1}{n}\sqrt[n]{\prod_{k=1}^{n}(n+k)}=\lim_{n\to\infty }\frac{1}{n}\sqrt[n]{\frac{2n!}{n!}}$](/mathtex/c9/c906c5e660b4502165fc1ba0c7ad24ad.gif)
![kopírovat do textarea $Q = \lim_{n\to\infty }\frac{1}{n}\sqrt[n]{\frac{\sqrt{4\pi n}(\frac{2n}{\mathrm{e}})^{2n}}{\sqrt{2\pi n}(\frac{n}{\mathrm{e}})^{n}}}\cdot \sqrt[n]{\frac{2n!}{\sqrt{4\pi n}(\frac{2n}{\mathrm{e}})^{2n}}} \cdot \sqrt[n]{\frac{\sqrt{2\pi n}(\frac{n}{\mathrm{e}})^{n}}{n!}}$](/mathtex/02/02300ffc60f44ee375f640f4c823a984.gif)
 pak také
pak také ![kopírovat do textarea $\lim_{n\to\infty }\sqrt[n]{b_n}=1$](/mathtex/87/8776a0aacd9a9921661f7da94f49a8e5.gif) .
.![kopírovat do textarea $\lim_{n\to\infty } \sqrt[n]{\frac{2n!}{\sqrt{4\pi n}(\frac{2n}{\mathrm{e}})^{2n}}} =1$](/mathtex/8a/8a49a229e380913cfc44951409915d1f.gif)
![kopírovat do textarea $\lim_{n\to\infty } \sqrt[n]{\frac{\sqrt{2\pi n}(\frac{n}{\mathrm{e}})^{n}}{n!}}=1$](/mathtex/73/73ebb20a9b959e957f9d85dea4520ff8.gif)
![kopírovat do textarea $Q=\lim_{n\to\infty }\frac{1}{n}\sqrt[n]{\frac{\sqrt{4\pi n}(\frac{2n}{\mathrm{e}})^{2n}}{\sqrt{2\pi n}(\frac{n}{\mathrm{e}})^{n}}}$](/mathtex/22/2268b568aeef7cd3463b28b8e3380a60.gif)
![kopírovat do textarea $\lim_{n\to\infty }\frac{1}{n}\sqrt[n]{2^n\Big(\frac{2n}{\mathrm{e}}\Big)^n}=\lim_{n\to\infty }\frac{1}{n}\cdot 2\cdot \frac{2n}{\mathrm{e}} = \frac{4}{\mathrm{e}}$](/mathtex/f3/f37ff461e85b2dc2eac3610492c82fe4.gif)

 je postupnost ostro kladnych realnych cisiel, a sucin v jej vyraze, nas moze inspirovat vysetrit postupnost
je postupnost ostro kladnych realnych cisiel, a sucin v jej vyraze, nas moze inspirovat vysetrit postupnost 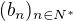 kde
kde  .
.![kopírovat do textarea $a_n= \sqrt [n]{\prod_{k=1}^n{(1+\frac kn)}}$](/mathtex/a8/a89a1a56358325def4859ed1ab5c0d67.gif)
 .
.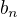 nie je nic ine ako Riemann-ov sucet, pre rovnomerne rozdelenie na [0;1] funkcii
nie je nic ine ako Riemann-ov sucet, pre rovnomerne rozdelenie na [0;1] funkcii  ktora je spojita a preto aj R-integrovatenana [0;1].
ktora je spojita a preto aj R-integrovatenana [0;1].![kopírovat do textarea $\lim_{n\to+\infty } b_n=\int_{0}^{1}\ln (1+x)dx =\int_{1}^{2}\ln (t)dt =[t\ln (t)-t]_{1}^{2}=\ln(\frac 4e)$](/mathtex/7f/7f7194d778ef11ff2a60cb86615d84c6.gif)

 .
.
 toho na výsledné limitě moc nezmění
toho na výsledné limitě moc nezmění se nachází alespoň 1 prvočíslo,
se nachází alespoň 1 prvočíslo, 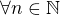 ,
, 

 je konstanta, lze ji tedy vytknout před limitu a součin rozdělit na součin limit:
je konstanta, lze ji tedy vytknout před limitu a součin rozdělit na součin limit: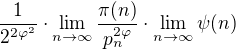

 je konstanta. Tedy
je konstanta. Tedy  je také konstanta.
je také konstanta. bude takové prvočíslo
bude takové prvočíslo 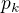 , že platí
, že platí  (zkrátka vemu nejblížší prvočíslo větší než číslo n).
(zkrátka vemu nejblížší prvočíslo větší než číslo n).
 je součin prvočísel, která jsme nevyužili. Pro n rostoucí do nekonečna tedy platí
je součin prvočísel, která jsme nevyužili. Pro n rostoucí do nekonečna tedy platí 



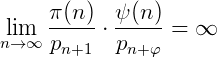
 a
a  ,
,