Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 05. 2008 16:00
Integrál
Mám za úkol zintegrovat funkci: 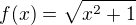
Moje řešení:
=========
Zkusil jsem použít 1. Eulerovu substituci (tj. 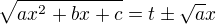 ), abych to převedl na integrál racionální funkce.
), abych to převedl na integrál racionální funkce.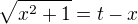
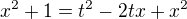
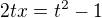
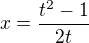
1) Použije se druhá substituční metoda (http://www.kubaz.cz/texty/KopacekMAI.pdf, str 149, věta 6.5)
značení: 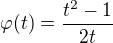 - Vezměme definiční obor
- Vezměme definiční obor 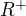 (oznacme ho I), obor hodnot je na tomto definičním oboru R
(oznacme ho I), obor hodnot je na tomto definičním oboru R
Definiční obor funkce f je také R, tím je splněn jeden požadavek věty.
Derivace: 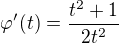 , tato derivace je pro každé t z definičního oboru kladná - tím je splněn druhý požadavek věty.
, tato derivace je pro každé t z definičního oboru kladná - tím je splněn druhý požadavek věty.
2) Vypočteme integrál: 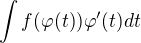 na R
na R
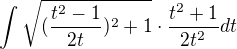
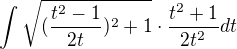
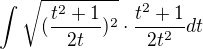
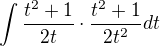
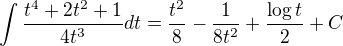 ... označme G(t)
... označme G(t)
Nyní se podíváme na 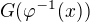 , která je naší požadovanou primitivní funkcí k f
, která je naší požadovanou primitivní funkcí k f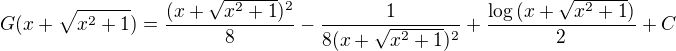
-----------------------------
Diky za pomoc
EDIT: opraveno podle prispevku nize
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#3 16. 05. 2008 17:06
Re: Integrál
↑ andrew: Díky, me slo predevsim o to zkusit to podrobne projit, jestli chapu spravne integral. Nicmeme na toto bych si nevzpomnel, jeste jednou diky
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#5 16. 05. 2008 17:28
Re: Integrál
↑ plisna: Takze bys postupoval, jako je to napriklad zde: http://www.mojeskola.cz/Vyuka/Php/Learn … okem10.php A v tom mem reseni vidis nejakou chybu?
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#6 16. 05. 2008 17:43
Re: Integrál
2Saturday : Jelikoz budu bit, nebot bych mel delat neco jinyho, ale... :) Chybu vidim zde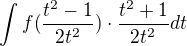 ma byt
ma byt  .
.
Dale se mi nezda ta inverzni fce 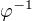 . Dle meho, by ses mel nejdrive zaobirat myslenkou, zda je
. Dle meho, by ses mel nejdrive zaobirat myslenkou, zda je  prosta na svym def. oboru. Coz neni. Navic, jak tak koukam na
prosta na svym def. oboru. Coz neni. Navic, jak tak koukam na  , tak algebraickymi upravami nepude vyjadrit inverzni.
, tak algebraickymi upravami nepude vyjadrit inverzni.
Offline
#7 16. 05. 2008 17:46
Re: Integrál
↑ andrew: Před chvilkou jsem to misto nasel take :) Myslel jsem, ze 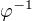 vyjadruje prevracenou hodnotu (inverzni funkci jsem take zkousel, ale protoze mi nesla, tak jsem se uchylil k myslence prevracene hodnoty)
vyjadruje prevracenou hodnotu (inverzni funkci jsem take zkousel, ale protoze mi nesla, tak jsem se uchylil k myslence prevracene hodnoty)
Aha, funkce phi neni prosta i kdyz je ta derivace kladna proto, ze je tam ten bod 0...
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#9 16. 05. 2008 19:35
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Integrál
↑ Saturday:
off topic: je jeste jedna metoda vypoctu tohoto integralu
Ostrogradskii: primitivni funkce je tvaru  , kde a,b,k jsou realne konstanty a daji se najit po zderivovani, prevedeni na rovnici mezi dvema polynomya porovnani koeficientu
, kde a,b,k jsou realne konstanty a daji se najit po zderivovani, prevedeni na rovnici mezi dvema polynomya porovnani koeficientu
Offline
#10 16. 05. 2008 21:10 — Editoval Saturday (17. 05. 2008 11:51)
Re: Integrál
SHRNU TO
========
1] Muj postup je spatne, protoze funkce phi neni prosta a i kdyby byla, tak nejde vyjadrit inverzni funkce, takze postup k reseni nevede.
EDITED: spatne, opraveno v puvodnim prispevku, kde je to dobre a funguje
2] Andrew navrhoval substituci: x = sinh t, ktera vede k cili opravdu rychle:
3] Diky ↑ plisnovi: za kompletni reseni ;-) (mimochodem, co je to za knihu, vypada to jako Jarnik, ale pri letmem projiti Jarnika jsem to v zadnem dile nenasel a nevim nic o tom, ze by napsal sbirku resenych prikladu ;-))
4] ↑ robert.marik: Diky :), je mozne nekde nakouknout do knihy od p. Ostrogradskiho?
5] Stale mi neni jasne, jestli pouziti Eulerovych substituci neni nekdy v rozporu s vetou o substituci u integralu => Ja jsem se na zacatku (marne) pokousel pouzit druhou metodu substituce, ktera vsak nefunguje. Podle jake vety je tedy vlastne mozne pouzit Eulerovy substituce?
EDIT:
ad 2] jeste slo vyjadrit arcsinh x
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#11 16. 05. 2008 21:37 — Editoval robert.marik (16. 05. 2008 22:14)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Integrál
↑ Saturday:
No, on toho napsal o integraci hodne. Tusim ze z jeho praci pak vzesly zaklady Rischova algoritmu, ktery se pouziva pro integraci v systemech pocitacove algebry. ta veta je pro integraly tohoto typu zformulovana v http://old.mendelu.cz/~marik/temp/int.pdf odstavec 7 - daval jsem sem ten odkaz pred par dny, ale teprve ted jsem nastavil spravne prava takze teprve ted to jde otevrit.... Odkaz bude platit minimalne tyden
Ostrogradskii rozpracoval hodne metod, jak primitivni funkci "uhodnout" a potom jenom doladit neurcite koeficienty. ale nic konretniho nemam. Mozna bude neco vic ve sbirce JIRÁSEK, FRANTIŠEK; KRIEGELSTEIN, EDUARD; TICHÝ, ZDENĚK, ale nemam ji ted po ruce, tak nemuzu rict presne.
Mozna bude mit nejake odkazy na tyto metody nekdo, kdo ma bliz k nasim vychodnim kolegum :)
ja jsem ted zkousel googlit ,ale ono je nekolik variant jak tohle jmeno prepsat do latinky, takze se hleda dost spatne. a jeho puvodni prace budou urcite dost stare, psane buh vi jakym jazykem (nasel jsem jednu citaci na dilo, ktere je francouzsky)
EDITACE:
http://mpec.sc.mahidol.ac.th/RADOK/phys … the%20form
zajimavost: Na teto strance pod Ostrogradskeho metodou oznacuji neco jineho, nez na co jsem se pod timto nazvem odkazoval ja. No jo, nekdo holt objevi tolik veci, ze v tom pak je binec .... :) Ale tak nad tou metodou "4.5.2 Ostrogradsky's method" premyslim a rikam si, proc se porad uci integrace racionalnich funkci tak blbe, s nasobnymi koreny ve jemnovatelich parcialnich zlomku, kdyz touto metodou to jde lip, hlavne pokud ty nasobne koreny jsou komplexni. No, promyslim, jestli tim pristi rok nepotrapit svoje krajinare a nabytkare:)
Offline
#12 16. 05. 2008 22:10 — Editoval Olin (16. 05. 2008 22:11)
Re: Integrál
Mno, já jsem kdysi integroval funkci 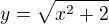 , a tehdy jsem využil úvahy, že je to akorát pootočený graf funkce
, a tehdy jsem využil úvahy, že je to akorát pootočený graf funkce 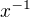 (což jsem předtím sáhodlouze dokazoval), kterou zintegrovat umím… A dál už to bylo snadné. Na případ s jedničkou to převedu asi substitucí.
(což jsem předtím sáhodlouze dokazoval), kterou zintegrovat umím… A dál už to bylo snadné. Na případ s jedničkou to převedu asi substitucí.
Offline
#13 16. 05. 2008 22:24
Re: Integrál
↑ robert.marik: Stahnul jsem si ;-) Zacina se mi doma kupit takove mnozstvi matematickeho materialu, ze z toho jde strach :))
BTW: Nevite odpoved na bod 5] v mem souhrnu vyse?
↑ Olin: Pootocenim grafu x^-1 graf funkce y=(x^2+2)^(1/2) nedostanes, ale mozna jsi tim pootocenim myslel jen neco jineho nez ja.
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#15 16. 05. 2008 23:01
Re: Integrál
↑ Olin: Muj graf mel automaticky skalovany osy.. kdyz se do grafu prikresli funkce f(x) = x a f(x) = -x, tak je to videt
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#16 16. 05. 2008 23:04 — Editoval robert.marik (16. 05. 2008 23:24)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Integrál

kde se nabralo to minus pred logaritmem?
off topic: a jeste jedna cesta substituce x=tan(t)
↑ Saturday:
a kde je teda problem? jak zni dotaz?
Offline
#17 16. 05. 2008 23:27
Re: Integrál
↑ robert.marik: otazka zni takto:
5] Stale mi neni jasne, jestli pouziti Eulerovych substituci neni nekdy v rozporu s vetou o substituci u integralu => Ja jsem se na zacatku (marne) pokousel pouzit druhou metodu substituce, ktera vsak nefunguje. Podle jake vety je tedy vlastne mozne pouzit Eulerovy substituce?
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#18 16. 05. 2008 23:27
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Integrál
Saturday napsal(a):
SHRNU TO
========
1] Muj postup je spatne, protoze funkce phi neni prosta a i kdyby byla, tak nejde vyjadrit inverzni funkce, takze postup k reseni nevede.
Ona je ta funkce ale prosta aspon nekde. A odkud nejde vyjadrit prosta funkce? Z te puvodni substituce jde prece vyjadrit i x i t.
Offline
#19 16. 05. 2008 23:31
Re: Integrál
↑ robert.marik: Nejde vyjadrit inverzni funkce k phi
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#20 16. 05. 2008 23:38 — Editoval robert.marik (16. 05. 2008 23:39)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Integrál
↑ Saturday:
Ale jde vyjadrit inverzi k phi pro kladna t. A to pro substituci staci. Phi bude definovana jenom pro kladna t.
Offline
#21 17. 05. 2008 01:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál
↑ robert.marik:↑ Saturday:
Papirove vydani najdete v zde, elektronika tady:
http://lib.org.by/get/M_Mathematics/Ost … 29_M_.djvu
http://lib.org.by/get/M_Mathematics/Ost … 29_M_.djvu
http://lib.org.by/get/M_Mathematics/Ost … 29_M_.djvu
Samotny proces stahovani je takovy pozvolny, ale byl prakticky odzkousen a zdarne dokoncen :-)
Offline
#23 17. 05. 2008 10:15
Re: Integrál
↑ robert.marik: Zvoral jsem to.. Ta funkce phi opravdu ma obor hodnot R na na definicnim oboru R+ a inverzni uz mam take vyjadrenou, takze stacilo vlastne jen dosadit. Opravil jsem to v puvodnim prispevku a po zderivovani primitivni funkce mi to opravdu da (1+x^2)^(1/2)
Takze to vypada, ze je to konecne hotove ;-) Diky moc vsem za pomoc :)
↑ jelena: Koukal jsem na ten web a nasel jsem tam i spoustu knizek na jine tema, tak si to postahuju :)
↑ plisna: Ono spousta knížek z matematiky, které za něco stojí jsou poměrně staré a dají se bohužel sehnat opravdu jen v antikvariátu. Například Jarník bych řekl, že je doteď nepřekonaný.
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline

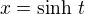 . Pripominam jen, ze plati
. Pripominam jen, ze plati  . Verim, ze uz ten integral snadno dopoctete.
. Verim, ze uz ten integral snadno dopoctete. , potom
, potom 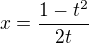 a
a 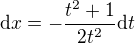 , pak uz to lze upravit a dokonce i zintegrovat :)
, pak uz to lze upravit a dokonce i zintegrovat :)
