Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 01. 2018 00:58 — Editoval liamlim (15. 01. 2018 01:09)
Něco jako teorie množin
Zdravím. Tak nějak jsem si vybudoval sám pro sebe "něco", o čem se trochu bojím říct, že je teorie. Protože si tím úplně nejsem jistý.
Chtěl bych, aby objekty mé teorie byly takové její formule, které mají jednou volnou proměnnou. Tedy aby pro libovolné dva objekty  a
a 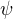 bylo
bylo 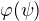 též objektem teorie.
též objektem teorie.
Je možné tento můj požadavek nějak formalizovat? Sám pro sebe si buduji něco jako teorii množin, takže bych chtěl, aby to celé bylo přímo v jazyce logiky. Co mě k tomu vedlo? V takové "teorii" uvažme následující definice (ne axiomy! žádný axiom není třeba):
> Rovnost definujme tak, že 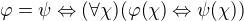
> Podmnožinu definujme tak, že 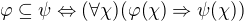
> Náležení definujme tak, že 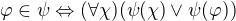
Co je možné z těchto definic triviálně odvodit:
1) axiom extenzionality: 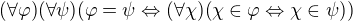
2) vztah podmnožiny a rovnosti: 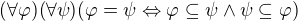
3) Jde triviálně odvodit fakt: 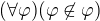 , čímž automaticky nemáme starost o jeden z typů paradoxů naivní teorie množin
, čímž automaticky nemáme starost o jeden z typů paradoxů naivní teorie množin
4) a další... třeba existence něčeho jako prázdná množina, atd
Moc prosím o informaci, jestli se někde v matematice taková teorie zkoumá. Připadá mi celkem přirozené když už mám teorii, kde jsou formule a jakési objekty, zkusit prostě a jednoduše namísto objektů použít znovu formule. Tím se otevře úžasná možnost skládání formulí a tedy naprosto přirozená definice pojmu náležení.
Offline
#2 16. 01. 2018 23:01
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Něco jako teorie množin
↑ liamlim:
Ahoj,
a) Vypadá to, že používáš predikátovou logiku druhého řádu, protože za argument dosazuješ i formuli, např. v těch definicích vidím nejen 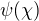 , ale i
, ale i 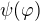 . Je to tak? Ideální je mít logiku prvního řádu, je-li to možné.
. Je to tak? Ideální je mít logiku prvního řádu, je-li to možné.
b) Je podstatné, že ty proměnné mají jen jednu volnou proměnnou? Neplatí to vše i pro formule s libovolným kladným počtem volných proměnných?
c) Není mi úplně jasná ta definice náležení, je to jen technická definice a nebo má i nějaký "význam"? A nemůže podle této definice potom pro nějaké formule platit 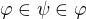 ? To bychom tu pak měli paradoxy...
? To bychom tu pak měli paradoxy...
"Máte úhel beta." "No to nemám."
Offline
#3 23. 01. 2018 20:39
Re: Něco jako teorie množin
↑ liamlim:
Zdravím,
ne, toto opravdu není teorie a nikdo se tím vážně zabývat nebude.
Předně mě zaujalo že "žádný axiom nění potřeba" :-) Bez axiomů nedokážeš nic (definice forlámího důkazu: Důkaz je posloupnost výrazů (většinou formulí - ale záleží na konkrétním kalkulu) kde každý výraz je buď axiomem, nebo je odvozen z předchozích pomocí nějakého z odvozovacích pravidel) - takže dokážeš maximálně tautologie logiky.
k těm triviálním dokazům, tak
1) je zase jen definice (lépe řečeno pospojování tvých definici), navíc ani nevidím jak by se to odvozovalo
2) obdobně jako předchozí bod, jen s tím rozdílem, že zde je odvozené zřejmé
3) není z tvého nijak odvoditelné a to ani kdybych se snažil být tolerantní a domyslel tam nějaký nevyřčený axiom - jak jsem upozornil výše
4) ani existenci prázdné množiny nedokážeš, ...
↑ check_drummer:
duhořádovou logiku bych nezatracoval. Ano máš pravdu, že je lépe se ji vyhnout, na druhou stranu už GB teorie množin je druhořádová a když se to vezme do důsledku, tak každá teorie s rovností je druhořádová.
Dva jsou tisíckrát jeden.
Offline
#4 24. 01. 2018 21:56 — Editoval check_drummer (24. 01. 2018 22:11)
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Něco jako teorie množin
↑ Wotton:
Zdravím. Ale co když ty definice kolegy liamlim přesně vystihují požadavky kladené na axiomy teorie množin? Třeba má logika druhého řádu takovou sílu, že je všechny dovede vyjádřit bez axiomů, tj. pomocí vhodných definic získáme to, co od predikátu náležení očekáváme...
Edit: Např. mějme nějakou teorii s nerovností ">", která je popsána nějakými axiomy. Následně definujeme predikát "<" pomocí predikátu ">" (x<y definujeme jako y>x) a přestože je to "jen" definice, pak pro takto zavedený predikát "<" odvodíme mnoho tvrzení. A co když je něco podobného i s těmi definicemi výše - i když zde můžeme využít jen ptostředky jazyka logiky a žádnou teorii.
"Máte úhel beta." "No to nemám."
Offline
#5 25. 01. 2018 21:33
Re: Něco jako teorie množin
↑ check_drummer:
Zde nejde o použitou logiku. Je třeba si uvědomit že definice je ve své podstatě jen zkratka za jiný zápis. A jako taková nemůže mít žádnou sílu, ani z ní nemůže nic plynout.
Dva jsou tisíckrát jeden.
Offline
#6 25. 01. 2018 21:49
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Něco jako teorie množin
↑ Wotton:
Co znamená, že z definice nemůže nic plynout? Když např. definuji nějaký predikát, tak můžu odvodit nějaké tvrzení, ve kterém se tento predikát vyskytuje.
"Máte úhel beta." "No to nemám."
Offline
#7 26. 01. 2018 16:32
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Něco jako teorie množin
↑ Wotton:
Ještě k teori s rovností - ta nemusí být druhého řádu, když nezavedeme axiom "pro každý predikát P platí (x=y) => (P(x)<=>P(y)" , ale když použijeme schema axiomů tvaru "(x=y) => (P(x)<=>P(y)" pro každý předikát P.
"Máte úhel beta." "No to nemám."
Offline
#8 31. 01. 2018 18:15 — Editoval Wotton (31. 01. 2018 18:17)
Re: Něco jako teorie množin
↑ check_drummer:
Tvrzení které dokážeš a ve kterém vystupuje definovaný pojem lze dokázat i bez tohoto pojmu. Jen jej budeš v tom tvrzení muset popsat tak jako v té definici.
Uvedu příklad:
v ZF máme například axióm potence, který tvrdí že ke každé množině existuje množina co má za prvky právě všechny podnožiny původní množiny.
Krom toho se zavádí Definice, kde se jen řekne že tý množině která existuje dle předchozího axiomu se bude říkat potence nožiny.
Nyní můžeme dokázat, že potence množiny má ostře větší mohutnost než množina původní (s použitím definice).
Ve skutečnosti se ale dokázalo, že množina včech podmnožin má ostře větší mohutnost než původní množina, a navíc o té množině víme že existuje.
Tyto dvě věty říkají to samé, jen jedna z nich je lépe čitelná, protože jsme použili definici potence. Neodvodili jsme díky ní ale silnější tvrzení (jen jsme obohatili jazyk).
↑ check_drummer:
S rovností je to takový hraniční.
Standartně se logika s rovností bere jako predikátová logika s přidanou relací = (kterou označíme jako rovná se) a přidáním axiomů rovnosti. Pak samozřejmě už prvořádová není. Na druhou stranu máš pravdu, že se to pro (některé) danné teorie dá obejít tím způsobem který jsi tu naznačil.
Je ale pak otázka zda to nazývat logikou s rovností nebo už pak je tato "rovnost" součástí zkoumané teorie.
EDIT: překlepy
Dva jsou tisíckrát jeden.
Offline
#9 31. 01. 2018 18:30 — Editoval liamlim (31. 01. 2018 18:32)
Re: Něco jako teorie množin
↑ Wotton:
↑ check_drummer:
Zdravím! Bohužel mi až teď přišel e-mail, že bylo reagováno na tento příspěvek, jinak bych se zajímavé diskuze zúčastnil mnohem dříve. Zkusím si tedy vzpomenout, co jsem před dvěma týdny vlastně experimentoval.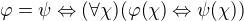
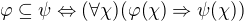
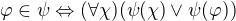
Toto jsou tři naše definice. První popíši, co jsou vlastně objekty této teorie. Objekty jsou prostě a jednoduše formule s jednou volnou proměnnou. Máme tedy objekty: 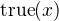 ,
, 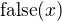 , které jsou konstantní formule s jednou proměnnou. Dále máme kupříkladu objekty
, které jsou konstantní formule s jednou proměnnou. Dále máme kupříkladu objekty  ,
, 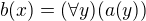 , atd.
, atd.
Vlastně je možné si říct, že každá formule  s jednou volnou proměnnou odpovídá množině
s jednou volnou proměnnou odpovídá množině 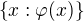 . Ty tři definice pak říkají následující:
. Ty tři definice pak říkají následující:
1) První definici můžeme chápat tedy jako 
Podobně druhý, třetí, atd. Důležité je, že výraz typu 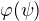 chápu jako
chápu jako 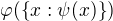 .
.
EDIT: Teď nemám úplně čas, ale slibuji, že se co nejdříve pokusím doplnit, jak jsem to celé myslel. Co je důležité:
Pokud připustíme, že vlastně množiny vůbec neexistují a pracujeme pouze s množinami, pak to má několik důsledků. Předně odpadají všechny množiny, které ve standardní teorii množin neumíme definovat.
Offline
#10 03. 02. 2018 10:55
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Něco jako teorie množin
↑ Wotton:
Ahoj,
jak je to s definicemi, je jasné - nezvyšují sílu teorie. Ale co když právě pomocí vhodné definice lze definovat teorii množin v samotné predikátové logice? Tedy jen pomocí vhodných definic již může být možné definovat pojmy jako "náležení", apod. a ukázat, že mají tytéž vlastnosti, jako mají stejné pojmy v "klasické" (ZF) teorii množin?
"Máte úhel beta." "No to nemám."
Offline
#11 03. 02. 2018 23:33
Re: Něco jako teorie množin
↑ check_drummer:
myšlenka hezká, ale ne. Tak to nejde. Ano, můžeš samojřejmě nadefinovat náležení, množinu, a třeba i nějaký vlastnosti, ... ale třeba nikdy jen v PL (s libovolnými definicemi) nedokážeš že existuje něco jako množina.
Dva jsou tisíckrát jeden.
Offline
#12 06. 02. 2018 13:35
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Něco jako teorie množin
↑ Wotton:
Ale to že to nejde, to už vypadá jako nějaké netriviální tvrzení. Protože v PL lze obecně dokázat mnoho výroků tvaru, že "něco existuje". Tak není na první pohled zřejmé, že by jedním z těchto výroků nemohlo být "existuje nějaká množina".
"Máte úhel beta." "No to nemám."
Offline
#13 06. 02. 2018 17:45
Re: Něco jako teorie množin
↑ check_drummer:
tak mi prosím předveď alespoň jediný.
A ber prosím v potaz model který má jednoprvkové univerzum, pro každou funkci tvého jazyka platí že tento jeden prvek je výsledkem jejího zobrazení a pro všechny predikáty platí, že aplikovaný na tento prvek (případně vícekrát) vznikne nepravdivý výrok.
A třeba si k tomu můžeš vzít model, který naopak z predikátů utvoří pravdivý výrok.
Oba tyto modely jsou modelem predikátové logiky bez axiómů, pro libovolný jazyk.
A asi je zřejmé nahlédnout, že žádná existencionální formule pro libovolnou vlastnost (krom x=x a tautologických popisů) opravdu nemůže platit v obou. Tudíž je nedokazatelná.
Dva jsou tisíckrát jeden.
Offline
#14 08. 02. 2018 21:34
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Něco jako teorie množin
↑ Wotton:
No já měl na mysli nějakou tautologii, nic jiného než tautologii totiž v PL nedokážeme...
"Máte úhel beta." "No to nemám."
Offline
#15 08. 02. 2018 21:51
Offline
#16 14. 02. 2018 22:01
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Něco jako teorie množin
↑ Wotton:
No ale to stále neznamená, že tvrzení o existenci množiny nemůže být nějaká tautologie PL.
"Máte úhel beta." "No to nemám."
Offline
