Matematické Fórum

↑ easy:

Zdravím,

A jaká je otázka?

Pokud "V kolik hodin se setkaji?" tak x_1=x_2, y_1=y_2

Nebo jiná otazka?

↑ easy:

Loď A se dostane do bodu se souřadnice  (x_a, y_a), loď B do bodu se souřadnici (x_b, y_b), vzdálenost bodů dle vzorce a postupu zde: http://forum.matweb.cz/viewtopic.php?pid=39927#p39927

Vzdálenost bodu je f(t), derivujeme a hledáme minimum funkce.

Stačí takto?

Stačí perfektně. Výsledek je 4.2

Děkuju

↑ asim:Kolineární vektory jsou takové různé vektory, které jsou rovnoběžné. Jediný rozdíl mezi těmito vektory je, že mají jinou velikost

u=(5,-3) , v=(v1,27)
Aby byly rovnoběžné, pak v=ku. Vidíme, že platí 27=-3k....k=-9 ( v2=-9u2). Toto musí platit i pro souřadnice u1,v1.
Takže v1=-9u1, v1=-9.5=-45

v=(-45;27)

↑ Rumburak:
Zdravím. Možná něco přehlížím, ale jediný rozdíl vidím ve slovíčku různé, které na té wikipedii chybí. Z hlediska selského rozumu je taková definice pravda přijatelnější. Je tam snad něco jiného co má zásadní smysl a dělá tam ještě nějaký větší rozdíl (který by se snad projevil v tomto případě)?

Jinak diskutovat definice do detailů, do toho bych se nerad pouštěl. Obě mluví o "rovnoběžnosti", kterou ale žádná z nich nedefinovala. My jsme si třeba ve škole nic jako rovnoběžnost vektorů ani nedefinovali, ten pojem se objevil pouze u variet.

↑ Rumburak:
Aha, chápu. Tu druhou část jsem právě bral jako "větu" a ne jako součást té definice, proto jsem ji nekomentoval. Máš samozřejmě pravdu.

Každopádně se shodneme na tom, že, přesně jak píšeš, pro laické pochopení to stačí, a pokud někdo na vysoké škole dělá zkoušku z lineární algebry (což je shodou náhod můj případ - příští týden), musí k tomu přistupovat stejně daleko důsledněji. Důsledněji myslím to, že pak už nestačí ani ta tvá definice rovnoběžnosti, protože je potřeba definovat přímku a směrový vektor (což nevyhnutelně vede k těm varietám, jak jsem zmiňoval - přímka je varieta o dimenzi 1 a směrový vektor libovolný vektor z jejího zaměření). Pak by ale řetězec definicí stejně musel pokračovat (varieta, zaměření, spojnice apod).
Ono podobným způsobem jde rozebrat většinu toho co se někde na internetu prezentuje jako matematická definice - skutečná důslednost je celkem vzácná. Proto mně to ani nedráždí a zvykl jsem si brát to s rezervou (rozcházející se definice atd). Teprve kdybych našel spor ve skriptech, začne mně to štvát.

Mimochodem by mně zajímalo... Jaká je teda ta "správná" definice kolinearity? Sice si tu hraju na chytrýho, ale my jsme si ten pojem nezaváděli. Hádám, že každý vektor je patrně kolineární sám se sebou (i když ta definice cos označil (1) to netvrdí). Ale jak je to třeba s nulovým vektorem? Je kolineární se vším, jenom sám se sebou, nebo s ničím?

↑ marnes:
:-) Nakolik do toho vidím, máš to dobře.

↑ LukasM:
Žádnou učebnici lineární algebry nemám k disposici, avšak díval jsem se do Rektorysova Přehledu užité matematiky,
kde v kapitole Vektorová algebra od Františka Kejly se píše:

Definice 7. Dva lineárně závislé vektory se nazývají kolineární (rovnoběžné), tři lineárně závislé vektory se nazývají komplanární.

Čekal jsem, že tam někde najdu i definici pro kollinearitu či komplanaritu BODŮ, ale nenašel jsem.


Osobně bych to pojal i obecněji:

1. Vektory u_1, ... , u_n  jsou kolineární právě tehdy, platí-li    dim Lin (u_1, ... , u_n)  <= 1 .
2. Vektory u_1, ... , u_n jsou komplanární právě tehdy, platí-li    dim Lin (u_1, ... , u_n)  <= 2 .

Symbolem Lin (u_1, ... , u_n) jsem označil lienární obal vektorů u_1, ... , u_n , sybolem dim pak dimensi příslušného prostoru.

3. Body A_1, ... , A_n  jsou kolineární právě tehdy, leží-li na společné přímce.
4. Body A_1, ... , A_n jsou komplanární právě tehdy, leží-li ve společné rovině (míněna je rovina dimense 2).

Ale nevím, jak dalece jsou takové definice "oficiální".

↑ LukasM:
Asi také podle toho, co je to varieta. Ten pojem znám spíše z analýzy případně z analytické a diferenciální geometrie, kde např. varietami
v E_3 jsou všechny rozumné křivky nebo plochy, což jistě daleko překračuje rámec daný lineární algebrou.

Z lineární algebry znám pojem LINEÁL V BODOVÉM PROSTORU  (bodový prostor B_n je jinými slovy eukleidovský prostor dimense n).
Jedna z možných definic lineálu:
Podmnožina L v B_n je lineál, jestliže existuje bod 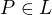takový, že množina je podprostor vekt. prostoru V_n.
Při tom V_n je množina všech translací (=posunutí) v B_n (a je vektorovým prostorem dimense n).
Modul W pak nazýváme zaměřením lineálu L. Je-li dim W =1, pak lineál L se nazývá přímka, atd.


Mám podezření, že "Tvá" varieta je totéž, co "můj" lineál -  pak sedí i definice rovnoběžnosti.  (Ve VŠ matematice neexistuje metodika, která by
byla až do detailů celostátně jednotná. Každá katadra a někdy i každý učitel má svoji, což je z určitého pohledu dobře, z jiného méně dobře.)

Slovo "kolineární"  v překladu znamené něco jako "spojeni jednou přímkou", což bych na lineály jakožto množiny neaplikoval.

↑ LukasM:Já Ti zase přeji šťastné pořízení u té zkoušky.