Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Integrace - složky rychlosti (TOTO TÉMA JE VYŘEŠENÉ)
#1 31. 01. 2018 15:39
Integrace - složky rychlosti
Dobrý den,
měl bych matematický/fyzikální problém, spíše ale ten matematický. Mohu se zeptat, zda tento integrál jde spočítat pouze s papírem a tužkou, případně jak ... vůbec mi totiž nejde do hlavy postup, co je ve skriptech.
Mockrát děkuji za radu
Offline
- (téma jako vyřešené označil(a) s-o-k-o-l)
#3 31. 01. 2018 20:18 — Editoval s-o-k-o-l (31. 01. 2018 21:02) Příspěvek uživatele s-o-k-o-l byl skryt uživatelem s-o-k-o-l. Důvod: nesmysl
#5 31. 01. 2018 21:34
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Integrace - složky rychlosti (TOTO TÉMA JE VYŘEŠENÉ)

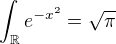 . Zajima te tohle, nebo to obskurni fyzikalni znaceni kolem?
. Zajima te tohle, nebo to obskurni fyzikalni znaceni kolem?