Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Střední škola
- » Exponencialni rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#51 06. 02. 2018 00:21
Re: Exponencialni rovnice
misaH napsal(a):
↑↑ Peter_CSR:
Naozaj máme len svoj čas. Všetci, nie iba zadávatelia.
Preto ho premrhajme na písanie "návodov" v prípadoch jednoriadkového riešenia
MATH IS THE BEST!!!
Offline
#52 06. 02. 2018 04:54
Re: Exponencialni rovnice
jarrro napsal(a):
misaH napsal(a):
↑↑ Peter_CSR:
Naozaj máme len svoj čas. Všetci, nie iba zadávatelia.Preto ho premrhajme na písanie "návodov" v prípadoch jednoriadkového riešenia
To som nenapísal ja, ale so sakazmom súhlasím :D .
Prvý krát som na tomto fóre mimo, netuším ktorá bije a keby mi niekto napísal postup bod po bode ušetrí mi dobrých 2 min času, za ktoré som mohol vyriešiť 4 iné príklady.... :/
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#53 06. 02. 2018 06:47 — Editoval misaH (06. 02. 2018 07:40)
- misaH
- Příspěvky: 13460
Re: Exponencialni rovnice
Hádať sa nemá zmysel. Samozrejme, že názory sa rôznia. Mnohokrát sa to tu diskutovalo... Je to o rešpekte k zabehaným dohodám.
Toto fórum nie je určené na poskytovanie kompletných riešení, to je všetko. Neviem, čo je na tom nezrozumiteľné.
Založte si fórum na poskytovanie kompletných riešení, keď sa vám to nepáči. Ešte aj tolerantný moderátor Stýv odkazuje žiadateľov kompletných riešení na pravidlá... (Klasika - prijímať migrantov aj keď presadzujú v cudzej krajine vlastnú kultúru alebo nie?)
A to, že Ty, Peter... by si vyrátal nejaké príklady navyše za čas, ktorý by si ušetril mňa osobne vôbec nezaujíma. Nie som na svete kvôli tebe. Trošku rešpektu - ľudia sem prispievajú dobrovoľne. Alebo aj neprispievajú. Viacerí výborní prispievatelia už odišli vďaka rôznym mudrcom....
Poskytovať kompletné riešenia by ma nebavilo. Je to nuda - a vedieť, že podporujem lenivosť, primitívnosť a drzosť by ma proste netešilo.
Offline
#54 06. 02. 2018 10:23 — Editoval Kubas126 (06. 02. 2018 10:40)
Re: Exponencialni rovnice
Ahoj,
můžu se prosím zeptat, jak postupovat při řešení těchto typů úloh?
chápu jak postupovat když by to byla kvadratická rovnica, ale u lineární rovnice vůbec nevím.
jen jsem zjistil, že když dosadim za x=-2, tak rovnice nemá řešení
nebo jestli se to řeší tím způsobem, že za x dosadím nulu?
to by mi pak parametr p vyšel , ale k čemu by mi to bylo?
, ale k čemu by mi to bylo?
Když dosadim za P jakékoliv číslo, tak mi vyjde x=-2
takže správná odpoved je asi za a?
Offline
#55 06. 02. 2018 10:53
Re: Exponencialni rovnice
↑ Kubas126:Pozor, neznama nie je  , ale
, ale  ,
,  je parameter, ktory pozname a riesenie vyjadrime pomocou neho. A k tvojej zaverecnej uvahe - mylis sa, ak napriklad
je parameter, ktory pozname a riesenie vyjadrime pomocou neho. A k tvojej zaverecnej uvahe - mylis sa, ak napriklad 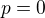 , tak
, tak  nebude
nebude  , skus si to.
, skus si to.
Offline
#56 06. 02. 2018 10:57
#57 06. 02. 2018 11:01 — Editoval vanok (06. 02. 2018 11:06)
Re: Exponencialni rovnice
Ahoj ↑ misaH:,
Mas pravdu v tom, ze treba respektovat pravidla fora.
Ale podla pravidiel fora:
Tvoj vyrok tykajuci migrantov sem nepatri.
Tak bud v buducnosti trochu pozornejsia ked nieco pises.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#58 06. 02. 2018 11:04
Re: Exponencialni rovnice
↑ Kubas126: Ano, spravne. A od teba sa chce, aby si zistil, ake bude  pri lubovolnom
pri lubovolnom  .
.
Offline
#59 06. 02. 2018 11:11
#60 06. 02. 2018 11:21
Re: Exponencialni rovnice
Ahoj, když už víš, že x = -2, v odpovědích jsou jen dvě možnosti, není určitě problém vybrat tu správnou. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#61 06. 02. 2018 11:28 — Editoval Kubas126 (06. 02. 2018 11:32)
#62 06. 02. 2018 11:38 — Editoval vlado_bb (06. 02. 2018 11:38)
Re: Exponencialni rovnice
↑ Kubas126: Danu rovnicu si uprav do tvaru  , pricom vyrazy
, pricom vyrazy 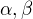 budu obsahovat
budu obsahovat  , co je v uplnom poriadku, lebo to je znamy parameter. A potom uz iba rozlisis pripady
, co je v uplnom poriadku, lebo to je znamy parameter. A potom uz iba rozlisis pripady  . A mas to.
. A mas to.
Offline
#63 06. 02. 2018 12:02 — Editoval Kubas126 (06. 02. 2018 12:10)
#64 06. 02. 2018 12:05 — Editoval misaH (06. 02. 2018 12:06)
- misaH
- Příspěvky: 13460
Re: Exponencialni rovnice
↑ Kubas126:
Nie.
Všetky x na 1 stranu.
Potom x vyňať.
Offline
#66 06. 02. 2018 12:14 — Editoval vlado_bb (06. 02. 2018 12:14)
Re: Exponencialni rovnice
↑ Kubas126: Nie. Urob to, co ti radi ↑ misaH:, pripadne po malych krokoch. Takze: roznasob lavu stranu v  a napis, co si dostal. Nic ine nerob, iba toto.
a napis, co si dostal. Nic ine nerob, iba toto.
Offline
#67 06. 02. 2018 12:19
#68 06. 02. 2018 12:23
#70 06. 02. 2018 12:29
Re: Exponencialni rovnice
↑ Kubas126: Vyborne, takze teraz roznasob lavu stranu rovnice  . Aku rovnicu dostanes?
. Aku rovnicu dostanes?
Offline
#72 06. 02. 2018 12:39
Re: Exponencialni rovnice
↑ Kubas126: Ano, teda  . Teraz postupuj dalej podla rady, ktoru si uz davnejsie dostal. Vsetky cleny obsahujuce
. Teraz postupuj dalej podla rady, ktoru si uz davnejsie dostal. Vsetky cleny obsahujuce  nechaj na lavej strane, ostatne daj na pravu. Co dostanes?
nechaj na lavej strane, ostatne daj na pravu. Co dostanes?
Offline
#74 06. 02. 2018 13:17
#75 06. 02. 2018 13:35 — Editoval Peter_CSR (06. 02. 2018 13:48)
Re: Exponencialni rovnice
↑ misaH:
Nie som si istý ako najlepšie to podať, tak to napíšem formou prosby: proste moje príspevky ignoruj. ďakujem :)
Budem zatiaľ žiť v slepej viere že je to dosť na to aby som sa ťa konečna zbavil :)
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
- Hlavní strana
- » Střední škola
- » Exponencialni rovnice (TOTO TÉMA JE VYŘEŠENÉ)


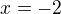



 . Co dostanes?
. Co dostanes?