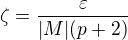Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Prázdninová nekonečná řada (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 07. 2009 10:33 — Editoval Marian (08. 07. 2009 10:37)
Prázdninová nekonečná řada
Zjistěte, zda-li existuje nekonečná řada reálných čísel 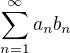 taková, že platí zároveň podmínky
taková, že platí zároveň podmínky
(1)  konverguje,
konverguje,
(2) 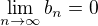 ,
,
(3) 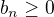 ,
,
(4) 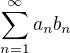 diverguje.
diverguje.
_____________
Pokud neexistuje, dokažte neexistenci, pokud existuje, najděte příklad.
Edit.: Podmínka (3) byla upravena ...
Offline
#2 08. 07. 2009 13:15
Re: Prázdninová nekonečná řada
↑ Marian:
Prvý pokus. Možno falošný dôkaz :-)
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 08. 07. 2009 14:06
Re: Prázdninová nekonečná řada
Domnívám se, že jako příklad funguje
Offline
#4 08. 07. 2009 15:05
Re: Prázdninová nekonečná řada
↑ lukaszh:
Taková řada existuje, jak uvádí a správně se domnívá kolega Rumburak, byť se to může zdát silně kolidující, pokud použijeme selský rozum. Opět jsem se ujistil u teorie nekonečných řad (a doufám, že i ostatní), jak může být fascinující, pokud se studují nekonečné řady reálných čísel obecně (nikoliv pouze s kladnými členy). Poučení z toho může plynout to, že cokoliv tvrdíte, je zapotřebí dokázat s přesností a jemnocitem a nespoléhat se na intuici.
Navíc v lukaszhově důkazu mi unikají sopuvislosti. V provedeném odhadu nesouhlasím s přechodem od parciálních součtů S_i k číslu M. Pokud chceme navíc používat Cauchyovo-Bolzanovo kriterium, je zapotřebí uvážit, že je zapotřebí dokázat podmínku z kriteria pro všechna přirozená čísla r, s taková, že ... Speciální volbou nepřesvědčíme nikoho.
Doporučuji ti podívat se příklad výše a provést ještě jednou tvé odhady na speciálním případě. Možná pak zjistíš, v čem je chyba.
↑ Rumburak:
Stejnou řadu jsem zkonstruoval také a potom už nebyl problém najít i jiné.
Všeobecně poznamenávám k této úloze, že by se mohlo zdát, že by fungovalo Abelovo kriterium. Jenže zde není zaručena monotonie posloupnosti kladných čísel {b_n}. Tedy tato podmínka nemůže být vypuštěna z Abelova kriteria. Protipříklad je v příspěvku ↑ Rumburak:.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Prázdninová nekonečná řada (TOTO TÉMA JE VYŘEŠENÉ)


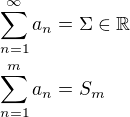

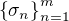 radu
radu 
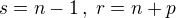 , odtiaľ
, odtiaľ je horné ohraničenie čiastočných súčtov. Číslo zeta treba zvoliť nasledovne
je horné ohraničenie čiastočných súčtov. Číslo zeta treba zvoliť nasledovne