Matematické Fórum

Vecerrov · 18. 02. 2018 20:02

Dobrý den,
myslím, že princip lineárních rovnic s absolutní hodnotou, ale tento příklad mi dělá problém.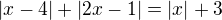
$|x-4|+|2x-1|=|x|+3$
Klasicky jsem určila nulové body: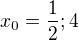
$x_{0}= \frac{1}{2};4$
Intervaly: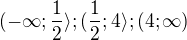
$(-\infty ;\frac{1}{2}\rangle;(\frac{1}{2};4\rangle;(4;\infty)$
Ty jsem označila jako:
$I_{1},I_2,I_3$
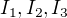
Pro první interval: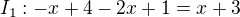
$I_{1}: -x+4-2x+1=x+3$
$4x = 2$
$x = \frac{1}{2}$
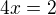
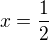
toto číslo je součást řešení
Pro druhý interval: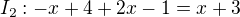
$I_2: -x+4+2x-1 = x+3$
$0 = 0$
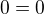
nekonečně mnoho řešení... to jsem zapsala jako ∞, tím si nejsem jistá, napsala jsem, že I_2 není součástí řešení
Pro třetí interval: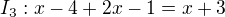
$I_3: x-4+2x-1=x+3$
$2x = 8$
$x = 4$
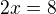
jelikož mám I_3 uzavřený, 4 nevyhovuje řešení

Z toho mi vychází jako jediné řešení 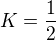$K={\frac{1}{2}}$
Jenže v učebnici je výsledek:
$K=\langle\frac{1}{2},4\rangle$

Předem moc děkuji všem za pomoc, snažila jsem se všechny své výpočty zapsat do dotazu aby odpovídající mohli snadno najít chyby a neměli zbytečně moc práce s opravou.
Díky!