Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 03. 2018 02:00
Teorie množin 2
Ahoj. Uvažme následující pravidla:
Nechť  ,
,  jsou množiny. Pak:
jsou množiny. Pak:
-  je dobré.
je dobré.
-  je dobré.
je dobré.
Nechť  ,
,  jsou dobré. Pak:
jsou dobré. Pak:
-  je dobré.
je dobré.
-  je dobré.
je dobré.
-  je dobré.
je dobré.
Nechť  je dobré,
je dobré,  je libovolná formule a
je libovolná formule a  je množina. Pak:
je množina. Pak:
-  je množina.
je množina.
-  je množina.
je množina.
Myšlenka: Myšlenka je, že dobré formule jsou navrženy tak, že se jedná o co možná největší skupinu formulí, ze kterých nejde postavit negace. Prostě a jednoduše žádnou kombinací konjunkce, disjunkce a ekvivalence člověk nedostane negaci.
Vím, že některé teorie formule takto limitují, že ale trpí nízkou expresivitou. Pak existují jiné teorie, které spoléhají na axiom vydělení. Ty mají samy o sobě bez přidaných axiomů problémy kupříkladu s definicí sjednocení množin. Zaráží mě ale, že jsem neviděl důkladně rozebranou teorii, která k axiomu vydělení přidává definici množiny skze obecnou "dobrou" formuli, která díky své "dobrosti" zjevně nemůže páchat problémy. Proto se ptám, co je tím důvodem? Mně připadá ono spojení jako celkem logická možnost, chci-li si zachovat co možná největší volnost v chápání, co vše je množina.
Offline
#2 09. 03. 2018 17:03
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Teorie množin 2
↑ liamlim:
Ahoj, a není to tím, že negace je tak důležitá, že teorie bez ní jsou příliš slabé ať jsou jakékoliv?
"Máte úhel beta." "No to nemám."
Offline
#3 09. 03. 2018 19:19 — Editoval Rumburak (09. 03. 2018 19:20)
Re: Teorie množin 2
Zaráží mě ale, že jsem neviděl důkladně rozebranou teorii, která k axiomu
vydělení přidává definici množiny skze obecnou "dobrou" formuli
Například Goedel Bernaysova TM , v níž primitivními pojmy jsou třída a náležení (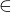 ) ,
) ,
je množina definována jako taková třída, která je zároveň prvkem nějaké třídy,
formálně
 .
.
Ony třídy, které nejsou množinami, nazýváme vlatními třídami, což je například
třída všech ordinálních čísel (chceme-li dát příklad ne ten nejtriiviálnější).
Offline
