Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 03. 2018 20:44
Kouzelny sud
Princ dostal od carodeje za ukol rozsvitit kouzelny sud. Jak uz nazev napovida, neni to obycejny sud. V sudu jsou ze shora ctyri diry umistene do tvaru ctverce (viz obrazek). Na dne kazde diry je jedna sklenice. Nektere ze 4 sklenic jsou dnem vzhuru, nektere dnem dolu. Na zacatku urcite nejsou vsechny sklenice dnem stejne. Princ ma za ukol otacet sklenicema tak, aby byly vsechny dnem stejne. Jakmile se mu to povede, sud se roztoci a nasledne rozsviti. Nicmene, neni to tak lehke... Nejdrive se sud roztoci. Kdyz se zastavi, princ muze sahnout do dvou libovolnych der a otocit obe, jednu nebo zadnou sklenici (jine sklenice nevidi). Potom se opet sud roztoci a bud se rozsviti nebo zastavi a princ muze opet sahnout jen do dvou der (a diky roztoceni nevi presne do kterych sahal pred tim). Pokusu ma neomezene. Muze se mu ukol podarit? Existuje strategie vedouci k jistemu uspechu? (Pozn: Hadanku jsem sem dal pro pobaveni, nepotrebuju pomoci s jejim resenim.)
Offline
- (téma jako vyřešené označil(a) laszky)
#2 21. 03. 2018 21:26
Re: Kouzelny sud
Já bych sahal do náhodně vybrané díry a otáčel sklenici dnem nahoru - a moc bych se divil, kdyby se mi to po pár pokusech nepovedlo, ale s jistotou to samozřejmě není (i když myslím, že je větší pravděpodobnost, že mi spadne během experimentu letadlo na hlavu, než že se mi to nepodaří...)
Ty dvě ruce se musejí do děr strkat najednou, nebo je lze strkat postupně (a nebo na tom nezáleží) ?
Nicméně jsem na řešení docela zvědavý, protože mě napadá jednoduchý argument proč by to s jistotou jít nemělo.
Protože podle mě existují jen dvě principiálně odlišné varianty, kam ruce strčit, buď do dvou sousedních děr, nebo do těch na uhlopříčce. No a ať to budeme střídat jak chceme, vždy se může sud zastavit tak nešťastně, že se rukama budeme pořád trefovat do stejných dvou párů děr (a k té čtvrté se nikdy nedostaneme).
Offline
#4 21. 03. 2018 22:53
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Kouzelny sud
↑ laszky:
Ahoj, pro úplnost - může se rozhodnout, které sklenice otočí až poté, co zjistí, v jaké poloze se sklenice v těch dvou dírách, do kterých sáhl, nacházejí? Tedy - vyberu si dva otvory - sáhnu tam - a až nyní se rozhodnu jaké sklenice otočím.
Řekl bych, že mohu, ale radši se ptám.
"Máte úhel beta." "No to nemám."
Offline
#5 21. 03. 2018 23:27
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Kouzelny sud
"Máte úhel beta." "No to nemám."
Offline
#6 21. 03. 2018 23:28 — Editoval laszky (21. 03. 2018 23:32)
Re: Kouzelny sud
↑ check_drummer:
Ahoj. Ano, to je spravne ;-)
A na tu prvni otazku je odpoved, ze samozrejme muzes ;-)
Offline
#7 22. 03. 2018 09:15
Re: Kouzelny sud
No dobře, tak to pojďme zkusit. Sud si můžeme napsat jako uspořádanou čtveřici nul a jedniček, třeba jako![kopírovat do textarea $[0,1,0,0]$](/mathtex/aa/aa637a9eae22a47a511acc1134d24cb7.gif)
Jednotlivé otvory jsou pozice 0, 1, 2, 3 (já jsem zvyklý počítat od nuly, pokud je to probém, můžeme počítat i od jedničky). Otáčení sudu bude cyklická záměna těch čísel.
Stačí říct, do kterých otvorů hodláte v příštím tahu strčit ruce (jako třeba do otvoru 0 a 3), a já pak sudem "zatočím".
Potom napíšete, co jste vykonali (kterou skleničku otočili a kteoru né). A do kterých otvorů strčíte ruce příště.
(prostě musíte napsat, do kterých otvoru strčíte ruce a teprve potom si otočím sudem - samozřejmě že né náhodně, ale abych vám to co nejvíce komplikoval). I první kombinaci sklenic vymyslím až poté, co budu vědět, to kterých otvorů strčíte ruce.
Tak do toho. (protože mě to nějak pořád nevychází).
Offline
#8 22. 03. 2018 11:33 — Editoval Ferdish (22. 03. 2018 11:35)
#9 22. 03. 2018 12:58 — Editoval Honzc (22. 03. 2018 13:29)
Re: Kouzelny sud
↑ laszky:
Zdravím,
tato úloha předpokládá, že princ sice na sklenice nevidí, ale hmatem pozná zda ta, na kterou šáhne je dnem vzhůru nebo dolů. Pak k vyřešení je potřeba maximálně 5 kol (kolem se myslí jedno otáčení sklenic)
Existuje i varianta úlohy taková, že princ na sklenice nesahá (neví tedy v jaké poloze jsou) a pouze dává příkazy někomu jinému, kterými sklenicemi má otáčet (ten ovšem musí mlčet o poloze sklenic)
Pozn. Někdy je tato úloha nazývána "Úloha slepého barmana s boxerskými rukavicemi"
Řešení dám případně později.(jenom řeknu, že v takovém případě je potřeba maximálně 7 kol)
Offline
#11 22. 03. 2018 13:11 — Editoval Honzc (22. 03. 2018 13:16)
Re: Kouzelny sud
↑ Ferdish:
A co když se sud bude stále zastavovat v poloze takové, že ty budeš stále sahat na stejné sklenice?
Offline
#12 22. 03. 2018 13:14 — Editoval Honzc (22. 03. 2018 13:18)
Re: Kouzelny sud
↑ MichalAld:
No asi na úhlopříce k té první co osahal - trochu jsem ti to zčeštil.
Offline
#13 22. 03. 2018 14:12 — Editoval Ferdish (22. 03. 2018 14:14)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Kouzelny sud
↑ Honzc:
Samozrejme, mohlo by to nastať, ale z hľadiska štatistického rozdelenia skôr či neskôr nastane prípad, kedy nahmatám práve tú druhú dvojicu...navyše úloha neznela, že mám nájsť minimálny počet kôl, kedy úlohu jednoznačne vyriešim, iba či je to možné.
Ja si myslím, že môj spôsob rozdelí tie štyri poháre na dve oddelené, jednoznačne rozlíšiteľné dvojice, avšak v tvojom postupe tú jednoznačnosť nejak nevidím...je síce tiež zaujímavý, ale budem sa musieť nad ním trochu viac zamyslieť, prípadne si to odskúšať na reálnej situácii, lebo len takto narýchlo "od brucha" v práci mi to nejak nejde do hlavy :-)
Offline
#14 22. 03. 2018 14:26 — Editoval Honzc (22. 03. 2018 14:30)
Re: Kouzelny sud
↑ Ferdish:
Pravděpodobnost bych sem nepletl.
Otázka pro řešení zní: " ....Existuje strategie vedouci k jistemu uspechu?..."
Offline
#15 22. 03. 2018 15:22
Re: Kouzelny sud
Tady se to pekne rozjelo...
↑ Honzc: Dik za odkaz na barmana, zrejme se jedna o verzi stejne hadaky, ale pro dospele :)
↑ MichalAld: K tomu tvemu argumentu, ze muzes strkat ruce stale do stejnych der... Ano, muze se stat, ze do jedne z der ani jednou nesahnes. (Kdyz budes sahat stale do stejne uhlopricky, resp. stejne ne-uhlopricne dvojice der). Ale to nevadi, proste tim postupem, ktery nastinil check_drummer nebo Honzc, ty zbyle tri sklenice postavis do stejne polohy, jakou ma ta sklenice v dire, kam jsi ani jednou nesahl.
Offline
#16 22. 03. 2018 18:23 — Editoval Ferdish (22. 03. 2018 18:23)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Kouzelny sud
↑ Honzc:
Díky...presne takto podrobne som to potreboval :-)
Apropo k tej pravdepodobnosti - prečo ju sem nepliesť? Ponúka tiež riešenie, aj keď nie optimalizované na minimálny počet ťahov, kedy úlohu bez ohľadu na počiatočné usporiadanie vyriešim so 100%-nou istotou.
Pokiaľ by však človek nemal veľa času (alebo trpezlivosti) na to, aby premyslel to riešenie do dokonalosti tak ako si ho uviedol ty, tak aj moje je použiteľné.
Ono totiž pravdepodobnosť, že n-krát za sebou siahnem na rovnakú dvojicu pohárov, je 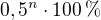 , čo pre n=5 dáva po zaokrúhlení na dve desatinné miesta pp rovnú 3.13 % a pre n=7 dokonca 0.78 %, čo je pre praktický účel dostatočne blízko :-)
, čo pre n=5 dáva po zaokrúhlení na dve desatinné miesta pp rovnú 3.13 % a pre n=7 dokonca 0.78 %, čo je pre praktický účel dostatočne blízko :-)
Offline
#17 23. 03. 2018 10:30 — Editoval Honzc (23. 03. 2018 10:31)
Re: Kouzelny sud
↑ Ferdish:
Tvá polemika je sice hezká, ale úlohu neřeší. Navíc když budeš řešit tu úlohu, že nebudeš vědět jak sklenice stojí (nebudeš je moct osahat-nevíš tedy zda je dnem dolů nebo nahoru), tak ji podle mě nevyřešíš.(nebo vyřešíš pouze velkou náhodou)
Offline


