Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 15. 04. 2018 10:58
Re: Vyňatie X
↑ 4pepo4: Nepises sice, s cim mas problem, ale podla nazvu temy usudzujem, ze z tohoto vyrazu chces vybrat  . Vedel by si to urobit pri vyraze
. Vedel by si to urobit pri vyraze 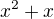 ?
?
Temu som presunul do kategorie Zakladna skola, nejde o ulohu tykajucu sa matematickych struktur.
Offline
#5 15. 04. 2018 11:42
Re: Vyňatie X
↑ 4pepo4: Aha, takze nejde o vynatie  , ale o jeho VYJADRENIE pomocou
, ale o jeho VYJADRENIE pomocou  , to je ina vec. Nakolko tu ide o kubicku rovnicu, najlepsie by asi bolo pre konkretne
, to je ina vec. Nakolko tu ide o kubicku rovnicu, najlepsie by asi bolo pre konkretne  pouzit nejaku pribliznu metodu, nezda sa mi schodne vyjadrit priamo
pouzit nejaku pribliznu metodu, nezda sa mi schodne vyjadrit priamo  ako funkciu
ako funkciu  a
a  .
.
Offline
#7 15. 04. 2018 11:44 — Editoval misaH (15. 04. 2018 11:45)
- misaH
- Příspěvky: 13467
Re: Vyňatie X
A je to teda originálne zadanie?
Podľa WA:
http://m.wolframalpha.com/input/?i=solv … E2%2Bx%5E3
Offline
#9 15. 04. 2018 12:08 — Editoval misaH (15. 04. 2018 12:08)
- misaH
- Příspěvky: 13467
Re: Vyňatie X
↑ vlado_bb:
Ahoj.
Pokojne maž, ak podľa Teba treba... :-)
Dúfam, že sa nehneváš - neviem si predstaviť, že takéto riešenie by "dal" "obyčajný" žiak...
Tá úloha je zvláštna, takže si myslím, že nie je pôvodná - no ale zadávateľ sa zatiaľ neozval.
Offline
#10 15. 04. 2018 12:24
Re: Vyňatie X
↑ misaH: Nie, to je v poriadku, ze si sem dala ten odkaz, ved uz sam zvazi, ci je to to, co potreboval. Bud je to uloha z praxe, a potom sa asi prikloni k pribliznemu rieseniu, alebo je to skolska uloha, a potom je zle zadana alebo zle opisana.
Offline
#14 15. 04. 2018 13:35
Re: Vyňatie X
↑ 4pepo4:
Ahoj. Tady je navod jak resit kubickou rovnici v Excelu. Pokud si chces nejakou metodu na hledani korene polynomu naprogramovat sam, potom muzes pouzit napr. Newtonovu metodu, ktera se pouziva pro libovolnou nelinearni rovnici, anebo muzes rovnou pouzit nejakou metodu pro hledani korene polynomu, jako je treba Graeffeho metoda, nebo Laguerreova metoda. Dalsi metody najdes napr. tady.
Offline


 ?
? 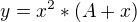 ale stále ma nenapadá, ako z daného vzorca by som vyňal neznámu
ale stále ma nenapadá, ako z daného vzorca by som vyňal neznámu 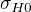
![kopírovat do textarea $\sigma _{H1}^{3}+\sigma _{H1}^{2}*[\frac{\gamma ^{2}*E}{24}*(\frac{a*z_{0}}{\sigma _{H0}})^{2}+a*E*(\nu _{1}-\nu _{0})-\sigma _{H0}]=\frac{\gamma ^{2}*E}{24}*(a*z_{1})^{2}$](/mathtex/dc/dc60033297b5f74825b86f458fb59a98.gif)
 pri rôznych podmienkach.
pri rôznych podmienkach.