Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 04. 2018 20:41 — Editoval stuart clark (01. 05. 2018 10:57)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
roots of function
If  is twice differentiable function on
is twice differentiable function on ![kopírovat do textarea $[a,e]$](/mathtex/4e/4ea52fad55306bc252df41ca1f2a1fb0.gif) and for
and for 
Then minimum number of roots of the equation  is
is
Offline
#2 28. 04. 2018 21:09 — Editoval laszky (02. 05. 2018 01:05)
Re: roots of function
Offline
#4 01. 05. 2018 10:58
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: roots of function
Please explain
If  is twice differentiable function on
is twice differentiable function on ![kopírovat do textarea $[a,e]$](/mathtex/4e/4ea52fad55306bc252df41ca1f2a1fb0.gif) and for
and for 
Then minimum number of roots of the equation  is
is
Offline
#5 02. 05. 2018 01:30 — Editoval laszky (02. 05. 2018 13:21)
Re: roots of function
↑ stuart clark:
Since  is non-negative and has zeroes at
is non-negative and has zeroes at  ,
,  and somewhere between
and somewhere between  ,
,  and
and  ,
, , there exist at least 6 roots of
, there exist at least 6 roots of  in
in ![kopírovat do textarea $[a,e]$](/mathtex/4e/4ea52fad55306bc252df41ca1f2a1fb0.gif) . Consequently, as in the previous case, there exist at least 4 roots of
. Consequently, as in the previous case, there exist at least 4 roots of  in
in ![kopírovat do textarea $[a,e]$](/mathtex/4e/4ea52fad55306bc252df41ca1f2a1fb0.gif) .
.
Offline
#6 03. 05. 2018 07:10 — Editoval stuart clark (03. 05. 2018 09:12)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: roots of function
Thanks ↑ laszky: But answer Given as  .
.
i have one doubt How can we assume function  in first question. (We can assume other function also like
in first question. (We can assume other function also like  type
type
Similarly How can we assume function  for second question. We can also assume other function.
for second question. We can also assume other function.
please clearfy me , thanks in advanced.
Offline
#7 03. 05. 2018 10:43
Re: roots of function
↑ stuart clark:
The crucial words are "at least". At first you have to notice that  , then you observe that
, then you observe that  for arbitrary
for arbitrary  and you choose
and you choose 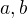 in such a way that
in such a way that  has maximal possible zeros. If you choose them wrong, you prove only partial result (not the optimal one) - like me in my previous answer. (I forgot that you can substract any linear function and substracted only constant). My approach is: draw a picture of the presumable graph of the function
has maximal possible zeros. If you choose them wrong, you prove only partial result (not the optimal one) - like me in my previous answer. (I forgot that you can substract any linear function and substracted only constant). My approach is: draw a picture of the presumable graph of the function  and then try to draw a line which intersects the function
and then try to draw a line which intersects the function  in maximal possible points.
in maximal possible points.
The following picture shows my first attempt with 6 zeros of the function g and my second attempt with 7 zeros of the function g (due to the zero derivative of  there are two intersections near the point
there are two intersections near the point  ). Hence, using this second attempt, we can prove that there exists at least 5 roots of
). Hence, using this second attempt, we can prove that there exists at least 5 roots of  . But 6 is still problem for me.
. But 6 is still problem for me.
Offline
 we find out that there exists at least 4 roots of
we find out that there exists at least 4 roots of 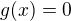 in
in  in
in  in
in 