Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 05. 2018 11:19
Osová souměrnost
Hezký den,
můžete mi prosím poradit, jek se dostanu k transformačním maticím osové souměrnosti dle přímky?
bod ![kopírovat do textarea $S=[0;0]$](/mathtex/3e/3e75909fce1dfe249f4bbd56e1ad821a.gif) se zobrazí do bodu
se zobrazí do bodu ![kopírovat do textarea $M=[1;5]$](/mathtex/5c/5c28ed8bbd00870a3bf710f260d28cb5.gif)
spojím body, udělám střed a pomocí normálového vektoru určím osu 
Teď ale nevím, jak pokračovat. Děkuji za pomoc
Offline
- (téma jako vyřešené označil(a) s-o-k-o-l)
#2 03. 05. 2018 17:23
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Osová souměrnost
Jak má vlastně v obecném případě ta operace zrcadlení kolem osy vypadat?
Je to něco jako , kde
, kde  je nějaká matice,
je nějaká matice,  je nějaký vektor,
je nějaký vektor,  je vektor, který zrcadlíme a
je vektor, který zrcadlíme a 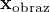 je jeho obraz?
je jeho obraz?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#3 03. 05. 2018 17:54
Re: Osová souměrnost
↑ s-o-k-o-l:
Potrebujes najit matici  a vekor
a vekor 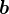 ve vztahu
ve vztahu  .
.
Je zrejme, ze 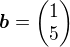
Matici  sestrojis tak, aby mela vlastni vektor
sestrojis tak, aby mela vlastni vektor  s prislusnym vl. cislem
s prislusnym vl. cislem  a vlastni vektor
a vlastni vektor  s vlastnim cislem
s vlastnim cislem 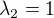 . Tzn., ze
. Tzn., ze  , kde
, kde
a .
.
Offline