Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Počítačové algebraické systémy (CAS)
- » Řešení rovnice eulerovou metodou (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 05. 2018 19:48
Řešení rovnice eulerovou metodou
Dobrý večer,
Mohl bych prosím požádat o pomoc s vyřešením rovnice k*R (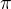 /2 -
/2 - ) = m*g*Sin (
) = m*g*Sin ( ) pomocí eulerovské metody se vstupními hodnotami R = 0.150, m = 1,k = 65, g = 9.8? Snažím se už nějakou chvíli následovat tutoriály, ale pokaždé jsem skončil s neúspěchem a nevím si už rady.
) pomocí eulerovské metody se vstupními hodnotami R = 0.150, m = 1,k = 65, g = 9.8? Snažím se už nějakou chvíli následovat tutoriály, ale pokaždé jsem skončil s neúspěchem a nevím si už rady.
Offline
- (téma jako vyřešené označil(a) zapnorak)
#2 05. 05. 2018 22:18
Re: Řešení rovnice eulerovou metodou
↑ zapnorak: Co mas na mysli pod Eulerovou metodou? Poznam metodu tohoto mena, ale ta sa pouziva na priblizne riesenie diferencialnych rovnic, cize ty mas na mysli nieco ine ...
Offline
#3 05. 05. 2018 22:33
Re: Řešení rovnice eulerovou metodou
↑ vlado_bb:
Omlouvám se moje chyba nějak jsem to celé popletl. Mělo by se to dát řešit pomocí bisekce což je pro mě snad ještě horší
Offline
#4 05. 05. 2018 22:34 — Editoval laszky (05. 05. 2018 22:35)
Re: Řešení rovnice eulerovou metodou
↑ zapnorak:
Nevim, jestli je to eulerovska metoda, ale zkusil bych tu rovnici trochu upravit...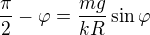
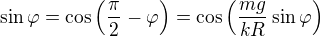
A ted bych uvazoval posloupnost 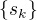 :
:
Ukaz, ze posloupnost konverguje, spocitej  a vysledek je
a vysledek je .
.
Edit: Neni to bisekce. Ale muzes si to zkusit.
Offline
#6 05. 05. 2018 22:51
Re: Řešení rovnice eulerovou metodou
Kdyz to chces pocitat pomoci bisekce, uvazuj funkci .
.
Pak  , zatimco
, zatimco  .
.
A uvazuj posloupnosti  a
a 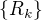 s
s  a
a 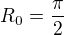
V kazdem kroku spocti 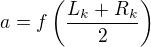 .
.
Pokud je  , potom
, potom 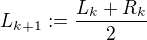 a
a  .
.
Pokud je  , potom
, potom  a
a 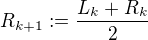 .
.
Obe dve posloupnosti  a
a 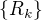 konverguji k reseni.
konverguji k reseni.
Offline
Stránky: 1
- Hlavní strana
- » Počítačové algebraické systémy (CAS)
- » Řešení rovnice eulerovou metodou (TOTO TÉMA JE VYŘEŠENÉ)
