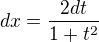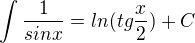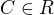Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » integral 1/sin(x) dx (TOTO TÉMA JE VYŘEŠENÉ)
#2 01. 08. 2009 12:18 — Editoval gladiator01 (01. 08. 2009 12:18)
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
Re: integral 1/sin(x) dx
čti a pak se ptej:
Code:
2) Pokud máte problém s nějakým integrálem, derivací nebo obyčejnou diferenciální rovnicí, zkuste před zadáním dotazu vyzkoušet některý z online-nástrojů. Například MAW vám standardní příklad spočítá i s postupem, a to v češtině. Dostanete tak okamžitou a podrobnou reakci. Seznam dalších nástrojů najdete v tématu Odkazy.
http://user.mendelu.cz/marik/maw/index.php?lang=cs&form=integral
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#4 01. 08. 2009 13:13 — Editoval Kondr (01. 08. 2009 13:20)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: integral 1/sin(x) dx
↑ Crusty:
substituce cos(x)=t, -sin(x)dx=dt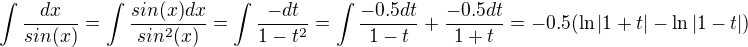 ,
,
teď stačí za t doplnit cos(x):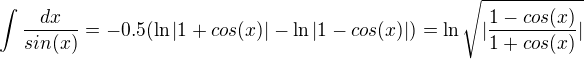
Existuje nekonečně nnoho způsobů, jak takový výsledek zapsat. Některé z těch hezčích využívají vzorců pro sin(x/2) a cos(x/2). Napiš výsledek ze sbírky a zjistíme, jestli je OK.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#8 04. 03. 2015 20:38 — Editoval misaH (04. 03. 2015 20:43)
- misaH
- Příspěvky: 13467
Re: integral 1/sin(x) dx
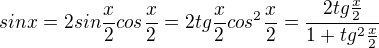
Nemôžeš sa pýtať presnejšie?
V druhom kroku sa využil vzťah pre dvojnásobný uhol.
V treťom sa sinus kvôli tangens delil kosínus, preto sa kosínus muselo hneď aj násobiť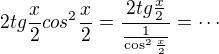
V poslednom menovateli sa 1 nahradí výrazom 
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » integral 1/sin(x) dx (TOTO TÉMA JE VYŘEŠENÉ)


 šipky jsou implikace
šipky jsou implikace