Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 05. 2018 23:49
Slabá Langrangeova věta
Už mi začíná být poměrně jasný důkaz u této věty a jsem si vědom jejího využití u vět O tečné nadrovině, Derivace složené funkce, ale rád bych jestli by mi někdo poradil slovy, co vlastně ona věta zařizuje. Její znění je následující:
Nechť 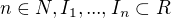 jsou otevřené intervaly,
jsou otevřené intervaly, 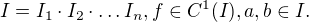 Potom existují body
Potom existují body  pro všechna
pro všechna 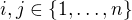 takové, že
takové, že 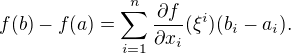
Offline
#3 26. 05. 2018 08:57
Re: Slabá Langrangeova věta
Řekl bych, že znění bude dobře, kdyžtak ho lze nalézt na stránkách http://www.karlin.mff.cuni.cz/~spurny/pages/fsv2.php jak je přednáška, verze pro tisk a v těch větách.↑ Bati:
Offline
#4 26. 05. 2018 09:03 — Editoval Bati (26. 05. 2018 09:11)
Re: Slabá Langrangeova věta
V poznamkach je f skutecne zobrazeni 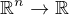 , takze jsem presvedcen, ze staci jedno xi a ta veta v poznamkach je blbe...
, takze jsem presvedcen, ze staci jedno xi a ta veta v poznamkach je blbe...
Resp. ta veta plati, ale staci vzit vsechny xi rovny tomu, co jsem napsal.
Taky je pak zrejmy, ze misto toho kvadru muzu vzit libovolnou konvexni mnozinu (a i to by se asi dalo zeslabit na souvislou)
Offline

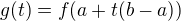 ,
, 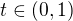 , tak dostanes
, tak dostanes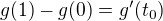
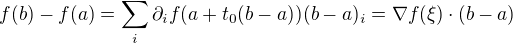 ,
,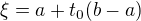 .
.