Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 06. 2018 13:07
Re: Definiční obor
↑ Waxion:
Hezký den.
Řekl bych, že podmínky pro výraz pod odmocninou by měly být
nebo
A ten prostřední interval v celkovém výsledku zřejmě nebude zcela správný (neplatí třeba pro x = 0).
Pokud se tedy nemýlím.
Offline
#3 18. 06. 2018 13:59 — Editoval Rumburak (18. 06. 2018 14:11)
Re: Definiční obor
↑ Waxion:
Ahoj.
Pokusím se Tvůj postup okomentovat. Máme určit definiční obor funkce 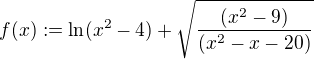 .
.
Tvůj postup:  správně
správně ŠPATNĚ : nerovnosti tvaru
ŠPATNĚ : nerovnosti tvaru  , kde
, kde 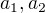 jsou navzájem různá čísla,
jsou navzájem různá čísla,
vůbec nezavádíme - když se nad tím zamyslíš, pochopíš, proč. 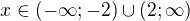 správně - příslušnou množinu označme
správně - příslušnou množinu označme 
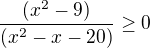 správně
správně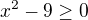
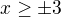 ŠPATNĚ - tatáž chyba, jako výše
ŠPATNĚ - tatáž chyba, jako výše správně - příslušnou množinu označme
správně - příslušnou množinu označme 
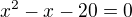

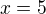
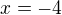
 správně - příslušnou množinu označme
správně - příslušnou množinu označme  .
.
ZBÝVÁ přesně určit průnik 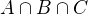 - třeba zakreslením uvedených množin
- třeba zakreslením uvedených množin
na číselnou osu. Zjistíme, že  .
.
Offline