Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Zvětšující se vzdálenosti obrazu omezené množiny
#1 10. 07. 2018 23:34 — Editoval check_drummer (14. 07. 2018 22:03)
- check_drummer

- Příspěvky: 4896
- Reputace: 105
Zvětšující se vzdálenosti obrazu omezené množiny
Ahoj,
nevím jestli je to přímo na analýzu, zde je zadání:
Nechť A je omezená množina v Rn (pro nějaké n). Existuje (pro nějaké n) funkce f z A do A (nemusí být surjektivní) taková, že pro každá různá x,y z A je vzdálenost(x,y)<vzdálenost(f(x),f(y))?
A pokud ano, tak:
1) Existuje taková f pro každé n?
2) Existuje taková f spojitá?
3) Existuje taková f pro souvislou, případně jednoduše souvislou množinu A?
4) (Dále uvažujte libovolnou kombinaci bodů 1)-3), na které je odpověď "ano".)
"Máte úhel beta." "No to nemám."
Offline
#2 11. 07. 2018 23:33
Re: Zvětšující se vzdálenosti obrazu omezené množiny
Pro spojitou funkci v n=1 si to představit moc nedokážu. Omezená množina (pokud tedy správně chápu, co to je) by měl být interval, a ta funkce by podle mě měla mít všude derivaci větší než 1 (nebo menší než -1) aby to platilo. Pak ale podle mě není možné, aby obor hodnot byl stejný interval.
No a nebo jednodušší úvaha (platící i pro vyšší hodnoty n a nespojité funkce) - když vyberu zrovna takovou dvojci bodů, jejichž vzdálenost je v rámci té množiny největší, těžko mohu dosáhnout toho, aby po zobrazení na nějaké jiné dva body byla jejich vzdálenost ještě větší (než největší). Tento argument ovšem platí jen pro uzavřené množiny. V otevřených množinách takovou dvojici bodů (s největší vzdáleností) nenalezneme.
Offline
#3 13. 07. 2018 01:36 — Editoval vanok (13. 07. 2018 12:05)
Re: Zvětšující se vzdálenosti obrazu omezené množiny
Ahoj ↑ check_drummer:,
Male poznamky.
Najprv treba povedat pre kazde  ;
; v tvojich podmienkach ...
v tvojich podmienkach ...
Inac ak  je ommedzena, tak musi existovat
je ommedzena, tak musi existovat  take ze
take ze 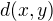 je maximalna. A co potom mozes povedat o
je maximalna. A co potom mozes povedat o  ?
?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 14. 07. 2018 22:04
- check_drummer

- Příspěvky: 4896
- Reputace: 105
Re: Zvětšující se vzdálenosti obrazu omezené množiny
↑ vanok:
Děkuji, pro různá x,y jsem doplnil do zadání, ale asi to bylo každému jasné, ýe je nutné shodné prvky neuvažovat.
To s tím maximem není správně, protože toho maxima se nabývat nemusí - bude existovat supremum, ale ne nutně maximum - vezmi si např. otevřený interval, apod.
"Máte úhel beta." "No to nemám."
Offline
#5 14. 07. 2018 22:08
- check_drummer

- Příspěvky: 4896
- Reputace: 105
Re: Zvětšující se vzdálenosti obrazu omezené množiny
↑ MichalAld:
Ahoj, spojitá funkce ale nemusí mít derivaci - dokonce v žádném bodě. :-) Ale možná by šlo provést nějakou úvahu, že f musí být monotónní...
S tím maximem je to tak - pro uzavřené množiny taková f neexistuje, ale my bychom chtěli prověřit všechny množiny, ne jen uzavřené.
"Máte úhel beta." "No to nemám."
Offline
#6 15. 07. 2018 01:29
Re: Zvětšující se vzdálenosti obrazu omezené množiny
↑ check_drummer:,
Tvoja mnozina A je obmedzena v Rn z beznou metrikou ?
Tak je cast gule konecneho polomeru v tom priestore.
Nema to suvis z tvojim problemom?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 15. 07. 2018 02:09
- check_drummer

- Příspěvky: 4896
- Reputace: 105
Re: Zvětšující se vzdálenosti obrazu omezené množiny
↑ vanok:
Ano, je to běžná metrika. Jen je A libovolná a pro tu chceme zjistit, zda taková funkce f existuje nebo ne.
Domněnka je, že taková spojitá f neexistuje.
Možná můžeme zatím uvažovat otevřenou kouli, třeba pro jednoduchost otevřený kruh nebo dokonce otevřený interval.
"Máte úhel beta." "No to nemám."
Offline
#8 15. 07. 2018 11:37
Re: Zvětšující se vzdálenosti obrazu omezené množiny
Zrovna jsem to chtěl napsat, že na otevřené množině (třeba otevřeném intervalu) ten argument s maximální vzdáleností použít nejde.
Ale stejně si myslím, že by to mělo jít nějak "hacknout", protože ta hranice má vůči původní množině nulovou míru, a třeba u toho intervalu si nedokážu představit, jak by to ty dva krajní body mohly zachránit.
Pokud funkce není diferencovatelná - to samozřejmě nevím, jak by se řešilo.
Offline
#9 15. 07. 2018 11:44
Re: Zvětšující se vzdálenosti obrazu omezené množiny
Mmch, před pár lety jsem na něco podobného narazil já - totiž, když se koukáme na měsíc (nebo slunce) nízko nad obzorem, připadá nám větší, než když je vysoko nebo přímo nad hlavou.
Lze dohledat, že je to jen optický klam, ale spousta lidí věří tomu, že dochází ke skutečnému zvětšení, že ta silná vrstva vzduchu nízko nad obzorem se chová trochu jako lupa.
A já tenkrát (tuším i na Aldebaranu) argumentoval tím, že není možné, aby vrstva vzduchu zvětšovala, a zároveň to dělala po celém obzoru stejně. Protože kolem dokola je to prostě 360° a z toho víc udělat nemůžeme. Nemůžeme dosánout toho, aby se jednotlivé stupně zvětšily (třeba každý na dva) a zároveň to dalo dohromady těch 360. Co někde "roztáhneme" bychom jinde museli "stlačit" - a to je zase v rozporu s tím požadavkem na symetrii.
Offline
#10 15. 07. 2018 13:40
- check_drummer

- Příspěvky: 4896
- Reputace: 105
Re: Zvětšující se vzdálenosti obrazu omezené množiny
↑ MichalAld:
Lze ukázat snadno, že f musí být prostá - a z toho už pro spojitou f na intervalu plyne, že musí být monotónní, z toho už asi půjde dokázat, že taková f požadované vlastnosti nemá.
Ve dvou rozměrech už bude situace asi složitější, protože "hranice" množiny A je nekonečná.
"Máte úhel beta." "No to nemám."
Offline
#11 15. 07. 2018 16:41 — Editoval vanok (15. 07. 2018 19:47)
Re: Zvětšující se vzdálenosti obrazu omezené množiny
↑ check_drummer:
Ak pre teba pojem funkcie povoluje, ze nie je vsade definonana potom
f taka, ze f(x)=2x pre x v intervale ]0; 1/2 [ a inde nedefinivana vyhovuje na intervale ]0;1[.
( no vsak ak musi byt definovana pre kazde x v ]0;1[ tak to neplati)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 16. 07. 2018 21:16
- check_drummer

- Příspěvky: 4896
- Reputace: 105
Re: Zvětšující se vzdálenosti obrazu omezené množiny
↑ vanok:
Ahoj, ano, musí být definována na celém A - ale nemusí být nutně surjektivní.
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Zvětšující se vzdálenosti obrazu omezené množiny
