Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 17. 08. 2018 16:24

žabí hněv
Příspěvky: 68
Reputace:   1 
 

Průběh funkce

Ahoj,

mám vyšetřit průběh funkce :$f(x)=x*cos(\frac{\pi}{x})$

Derivace mi vyšla $f'(x)=cos(\frac{\pi}{x})+\frac{\pi}{x}*sin(\frac{\pi}{x})$

Neporadil by mi prosím někdo, jak najít stacionární body, aniž bych to řešil nějakou numerickou metodou?

Děkuji

Offline

 

#2 18. 08. 2018 03:28

KennyMcCormick
Příspěvky: 1677
Reputace:   49 
 

Re: Průběh funkce

Podle mě to nepůjde, protože WolframAlpha vidí jenom numerické řešení.

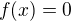Tady se můžeš podívat, jak ta funkce má vypadat, což by ti mohlo napovědět, jak se dostat k jejímu grafu (napadá mě např. najít fci, která fci $f(x)$ ohraničuje, nebo ukázat, že mění směr (klesající/rostoucí) na intervalu $[a;a]$ pro všechna $a>0$ nekonečně mnoho krát, najít řešení pro $f(x)=0$ (ale nevím, jak), atd.).

Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.

Offline

 

#3 18. 08. 2018 10:00

žabí hněv
Příspěvky: 68
Reputace:   1 
 

Re: Průběh funkce

↑ KennyMcCormick:

Díky.

Já jsem aplikoval Rolleovu větu na nulové body a maximum jsem hledal metodou pokus omyl.

Offline

 

#4 18. 08. 2018 13:31

jarrro
Příspěvky: 5465
Škola: UMB BB Matematická analýza
Reputace:   303 
Web
 

Re: Průběh funkce

$\cos{\(\frac{\pi}{x}\)}+\frac{\pi}{x}\cdot\sin{\(\frac{\pi}{x}\)}=0\nl \cos{\(t\)}+t\sin{\(t\)}=0\nl 1+t\mathrm{tg}{\(t\)}=0\nl \mathrm{tg}{\(t\)}=-\frac{1}{t}$
Ale elementárne riešenie to asi nemá

MATH IS THE BEST!!!

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson