Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Realne matice
#26 26. 08. 2018 13:12
Re: Realne matice
Čtyřvektory, symetrie a fyzikální zákony:
Od objevu teorie relativity se začalo věnovat hodně úsilí tzv. symetriím, jež se v přírodě vyskytují - protože se ukázalo, že je to docela dobrá cesta jak uhádnout další fyzikální zákony.
O co tedy jde - o to, že fyzikální zákony nezávisejí na některých "věcech". Například by neměly záviset na poloze v prostoru. Pokud vyrobíme nějaké zařízení, mělo by fungovat v Praze stejně jako v Brně, na Zemi stejně jako na Marsu, nebo i v jiné galaxii. Neřešíme samozřejmě, že na Marsu mohou být jiné podmínky (gravitace, např) než na Zemi. Jde o to, že pokud vytvoříme stejné podmínky, tak zařízení by také mělo fungovat stejně. Nezmění svoji funkci jen proto, že jsme jej v prostoru umístili někam jinam. Říkáme tomu "symetrie vzhledem k posunutí (poloze) v prostoru".
Stejně tak by mělo zařízeni fungovat stejně včera jako dneska nebo jako zítra. Nebo za milion let. Jeho funkce by neměla záviset na "poloze v čase".
Z takovýchto požadavků (nezávislost na poloze v prostoru ani v čase) nám plynou nějaké požadavky na matematický tvar fyzikálních zákonů. Jejich popis nemůže totiž obsahovat přímou závislost na prostorových či časových souřadnicích. Tedy na x, y, z a t. Může obsahovat pouze derivace podle těchto souřadnic.
Další symetrie, kterou náš svět má, je symetrie vůči natočení. Zařízení bude fungovat stejně, ať už jej (třeba ve volném vesmíru) natočíme jakým chceme směrem.
Matematicky zařídit, aby fyzikální zákony nezávisely na "natočení" je trochu složitější, než by se na první pohled mohlo zdát. Potřebujeme totiž dosáhnout toho, aby bylo jedno, jestli "natočíme" nejprve počáteční stav a z něj spočítáme výsledek, nebo jestli nejprve spočítáme výsledek a potom jej "natočíme". Potřebujeme dosáhnout toho, aby se nám "obě strany rovnice natáčely stejným způsobem". Abychom toho dosáhli, musíme použít matematické objekty zvané TENZORY. Příkladem tenzoru, co každý zná je VEKTOR. Pokud bude náš fyzikální zákon popsaný pomocí vektorů, můžeme být v klidu - všechny vektory se transformují stejně. Nezávislost na otočení bude zajištěna.
Můžeme v našich fyzikálních zákonech provádět i různé "kejkle" - můžeme vektory třeba násobit - skalárním součinem dvou vektorů dostaneme skalár, vnějším součinem vektorů dostaneme 2D tenzor (matici), a vše se pořád při otáčení transformuje tím správným způsobem. I diferenciální operátory mohou být vektory (gradient, divergence, rotace), také se transformují jako každý jiný vektor.
No a poslední, a z fyzikálního hlediska asi nejdůležitější (a nejméně intuitivní) je symetrie vůči "pohybu konstantní rychlosti". Pokud se naše zařízení bude pohybovat konstantní rychlostí, bude fungovat stejně, jako kdyby stálo (nebo se pohybovalo nějakou jinou rychlostí). Je to symetrie vůči Lorentzově transformaci.
Abychom tuto symetrii dokázali ve fyzikálních zákonech zajistit, musíme všechny zákony formulovat pomocí čtyř-tenzorů (třeba čtyř-vektorů), tak jako jsme symetrii vůči natočení zajistili pomocí tenzorů (třeba vektorů). A protože čtyřvektor se, co se týká prostorových souřadnic, chová jako vektor, zajistí nám použití čtyřvektorů automaticky i symetrii vůči obyčejné rotaci.
A pokud dodržíme i dříve zmíněný požadavek, že fyzikální zákony nesmějí explicitně záviset na poloze v prostoru a čase, máme "celkem jednoduchý" postup, jak mít naše fyzikální zákony v pořádku. Pokud budou formulovány pomocí čtyřvektorů (případně jiných čtyřtenzorů), budou konzistentní s teorií relativity.
No - je ještě jedna symetrie, o které se v klasické fyzice téměř nemluví - totiž symetrie vůči zrcadlení. Pokud bychom vyrobili zařízení, a potom jeho zrcaldový obraz, bude fungovat stejně, nebo nebude? V klasické fyzice zní odpověď ANO - jak Newtonovy (i relativistické) pohybové zákony, tak i rovnice elektromagnetického pole při zrcadlení nezmění tvar. Pravda - vektor magnetické indukce nám bude mířit na opačnou stranu, ale z toho žádný měřitelný důsledek nevzejde.
V kvantové mechanice je to ovšem jinak - ačkoliv všechny ostatní výše zmíněné symetrie tam platí bez výhrad, symetrie vůči zrcadlení už né. Některé rozpady ovládané slabými interakcemi tuto symetrii narušují. Nejlepším příkladem je polarizace neutrin, tam dochází ke 100% narušení symetrie, všechna neutrina mají jen jednu (levotočivou či pravotočivou, nevím z hlavy kterou) polarizaci, zatímco anti-neutrina mají zase tu druhou. A polarizace by se právě měla při zrcadlení otočit, zatímco částice se na anti-částici nemění.
Offline
#27 26. 08. 2018 13:24
Re: Realne matice
Symetrie a zákony zachování:
Poslední příspěvek k tomuto tématu. Matematička Amalie Emmy Noetherová objevila, že s každou symetrií (fyzikálních zákonů) se pojí jistá veličina, jejíž hodnota se ZACHOVÁVÁ. Dnes je to známé jako Teorém Noetherové.
Důkaz vyžaduje použití variačního počtu (hledání extrému funkcionálu), je to docela složitá věc...ale má jednoduchý důsledek - s každou symetrií se pojí veličina, jež se zachovává.
S nezávislostí fyzikálních zákonů na poloze je spojen zákon zachování hybnosti.
S nezávislostí na "poloze v čase" je spojeno zachovávání energie.
S nezávislostí na otočení je spojeno zachování momentu hybnosti.
No a s nezávislostí na pohybu konstantní rychlostí (s Lorenzovou symetrií) je spojen zákon zachování dost abstraktní "věci" zvené SPIN. Já popravdě ani nevím, co to přesně v klasické fyzice představuje, pojem se spíše používá v kvantové fyzice. Je to takové zvláštní, že ta nejdůležitější symetrie ve vesmíru zachovává "jen" takovou vysoce abstraktní věc.
Také jsem zmínil symetrii vůči zrcadlení, a s ní je spojena veličina zvaná PARITA. V klasické fyzice je to prostě jednička a nikdo se tím nezabývá, v kvantovém světě může nabývat dovu hodnot (+1, -1), sudá nebo lichá parita a je to docela důležitá věc.
V kvantové fyzice existuje celá řada dalších symetrií, které už nemají klasickou analogii, a k nim se váže i odpovídající řada zachovávajících se veličin.
Offline
#28 26. 08. 2018 13:26
Re: Realne matice
vanok napsal(a):
Ahoj ↑↑ MichalAld:,Mohol by si nam povedat nieco o priestorovych a casovych vektorovy v tomto priestore? A co su svetelne vektory?
Já úkol (nějak) splnil, teď jsi na řadě ty s grupami....HI.
Offline
#29 26. 08. 2018 19:06 — Editoval vanok (26. 08. 2018 19:53)
Re: Realne matice
Ahoj ↑ MichalAld:,
Ano urobil si pekne zrnutie tej teorie.
O grupach sa da vela hovorit. No skusme hovorit ( zatial) o tych co sa tykaju matic o ktore sa zaujimame.
No vsak neviem, ci je treba zacat hovorit o teorie grup uplne od zakladov, alebo ci uz nieco vies co by sme mohli pouzit?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#30 26. 08. 2018 20:31
Re: Realne matice
Offline
#31 27. 08. 2018 17:08 — Editoval vanok (28. 08. 2018 21:48)
Re: Realne matice
Ahoj ↑ MichalAld:,
Tak aby si sa do problemov tykajuce sa grup a v oblasts realnych matic ( zatial) dostal, tak ti dam urobit niekolko uvah na tu temu.
Uvazujme maticu  kde miera uhlu
kde miera uhlu  je
je 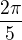
( iste si spoznal v A maticu rotace uhlu  )
)
Ak aplikujes tuto rotaciu na bod 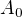 roviny suradnic (1; 0) ( v ortonormalnom systeme priamo orientovanom) tak co bude jeho obraz
roviny suradnic (1; 0) ( v ortonormalnom systeme priamo orientovanom) tak co bude jeho obraz  ?
?
A ak ju znovu aplikujes na bod 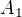 ? Atd.
? Atd.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#32 27. 08. 2018 23:15
Re: Realne matice
vanok napsal(a):
Ak aplikujes tuto rotaciu na bod
roviny suradnic (1; 0) ( v ortonormalnom systeme priamo orientovanom) tak co bude jeho obraz
?
V tom je nějaký trik, nebo je odpověď prostě bod o souřadnicích  ?
?
A když ještě jednou, dostaneme (asi)  , což se (asi) rovná
, což se (asi) rovná 
Offline
#33 28. 08. 2018 21:56
Re: Realne matice
Ahoj ↑ MichalAld:,
Urobil si celkom dobre pozorovanie.
V tomto specialnom pripade, 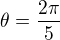 mozes konstatovat ak ju stale aplikujes na posledny bod co si dostal , ze tvoja rotacia sa bude periodicky opakovat.
mozes konstatovat ak ju stale aplikujes na posledny bod co si dostal , ze tvoja rotacia sa bude periodicky opakovat.
( body 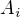 sa budu prechadzat po pravidelnom 5uholniku).
sa budu prechadzat po pravidelnom 5uholniku).
Ak to formalizujes uvidis, ze ide o jednu grupu.
Ako by si ju popisal?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#34 28. 08. 2018 22:21
Re: Realne matice
Mno, teď se dostáváme do bodu, kdy tak úplně přesně nevím, co se po mě vlastně chce.
Předpokládám, že prvky té grupy mají být ty matice - matice rotace o úhel  , nebo jeho N-násobky).
, nebo jeho N-násobky).
Taky bych řekl, že to N bude stačit v rozsahu 0, 1, 2, 3, 4.
Mezi těmi maticemi by měla existovat ta binární operace, né ? To odpovídá jejich násobení (skládání rotací).
Měl by existovat "jednotkový prvek" - to je ta matice pro N=0 (jednotková)
a ke každé matici by měla existovat inverzní matice, a to asi existuje (k N=0 je to ta samá, k N=1 je to N=4 a naopak, k N=2 je to N=3 a naopak).
Ještě mě napadá, že ty rotační matice pro jednotlivá N lze vlastně získat tak, že tu první (rotaci o úhel  ) umocníme na N.
) umocníme na N.
Dál už nevím, co mám dělat...
Offline
#35 29. 08. 2018 16:15 — Editoval vanok (29. 08. 2018 17:44)
Re: Realne matice
Ahoj ↑ MichalAld:,
Cize ta grupa ma 5 prvkov.
( je isomorfna z aditivnou grupou zvyskov delenia celych cisiel cislom 5: grupa modulo 5)
Ak sa z tym trochu pohrajes lahko urobis tabulku 5x5 vsetkych moznych operacii v tejto grupe. ( podobne ako ste iste robili tabulku malej nadobilky ...) Tu vsak kazdy vysledok ostane jedno z cisiel 0,1,2,3,4.
To sa ti zda jednoduche?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#36 29. 08. 2018 16:32
Re: Realne matice
To nějak řekněme chápu (modulové sčítání) - protože počítače takto počítají, takže když člověk programuje, tak to musí nějak brát v potaz. Že u 8-bitových procesorů je 255 + 1 = 0
Takže u grupy modulo 5 to bude předpokládám následovně:
0 + 0 = 0, 0 + 1 = 1, 0 + 2 = 2, 0 + 3 = 3, 0 + 4 = 4,
1 + 0 = 1, 1 + 1 = 2, 1 + 2 = 3, 1 + 3 = 4, 1 + 4 = 0,
2 + 0 = 2, 2 + 1 = 3, 2 + 2 = 4, 2 + 3 = 0, 2 + 4 = 1,
3 + 0 = 3, 3 + 1 = 4, 3 + 2 = 0, 3 + 3 = 1, 3 + 4 = 2,
4 + 0 = 4, 4 + 1 = 0, 4 + 2 = 1, 4 + 3 = 2, 4 + 4 = 3,
To je řekněme celkem jasné, a že to platí pro matice rotace o úhel 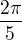 , to je asi taky jasné.
, to je asi taky jasné.
Že se ty matice rotace nesčítají ale násobí.
0 by měl být ten "neutrální prvek grupy"
1 by měla být inverzním prvkem ke 4, 2 ke 3 a naopak.
Offline
#37 29. 08. 2018 17:47
Re: Realne matice
↑ MichalAld:,
Je uzitocne si uvedomit, ze uhly rotacie sa scitaju modulo  ( nasobenie matic v tomto pripade
( nasobenie matic v tomto pripade 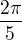 sa prevavi tym ze vysledok da scitanie uhlov ... preto som pouzil pojem idomorfismu)
sa prevavi tym ze vysledok da scitanie uhlov ... preto som pouzil pojem idomorfismu)
Tie tvoje vypocty mozes napisat aj do stvorcovej tabulky
No ako vidis, mas tu jeden priklad konecnej komutativnej grupy.
Dalsi priklad, cas sa casto pocita modulo 12.
Poznamka. Zatial hovorime len o operacii co sa podoba bezne scitanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#39 29. 08. 2018 18:17
Re: Realne matice
Cau ↑ MichalAld:,
Tak ostanme pri poslednom zapise.
Iste je ti jasne, ze 1 je generator tejto celej grupy.
Co znamena ze 2=1+1, 3=1+1+1,...takto dostanes vsetky jej prvky.
Su aj ine generatory tejto grupy?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#40 29. 08. 2018 18:32
Re: Realne matice
Přijde mi, že krom prvku 0 (kterým nic jiného než 0 nevygenerujeme) by všechny ostatní mohly být generátory:
Třeba 2:
2 + 2 = 4
2 + 2 + 2 = 1
2 + 2 + 2 + 2 = 3
2 + 2 + 2 + 2 + 2 = 0
A zdá se, že obdobnou hru lze hrát i s ostatními prvky (krom té nuly).
Ale mám intuitivní pocit, že když by to N bylo jiné, třeba 6, tak by už to takto nefungovalo, a třeba prvkem 2 už bychom všechno nevygenerovali.
Offline
#41 29. 08. 2018 19:30
Re: Realne matice
Ahoj ↑ MichalAld:,
Ked uz robime tie doplnky na grupu, tak pridajme male pozorovania.
Vseobecne ak pojde o grupy takeho isteho typu, ktore maju prvociselny pocet prvkov, alebo nie tak to da analogicku
v prvocislenych pripadoch a ako je v inych pripadoch?
Vysetri napr. pripad pre n=6.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#42 29. 08. 2018 22:18 — Editoval MichalAld (29. 08. 2018 22:25)
Re: Realne matice
OK, zkusím to. N = 6, tj prvky 0, 1, 2, 3, 4, 5
1 bude generátor vždycky, to je celkem jasné.
2 né, to vygeneruje jen 2, 4, 0
3 né, to zase jen 3, 0
4 né, to jen 4, 2, 0
5 asi ano, 5, 4, 3, 2, 1, 0
Zdá se být zřejmé, že pokud je N tím číslem dělitelné, tak to číslo nemůže být generátor.
Jestli se i na čtyřku vztahuje nějaké obecné pravidlo, to teď na první pohled nevidím.
(ještě by to mohlo být tak - ale je to čistě jen nápad, nijak jsem to neanalyzoval - že když nějaký prvek grupy je nebo není generátor, tak k němu inverzní prvek taky je nebo není generátor. Napadlo mě to, protože zrovna na počítačích se ta čísla často interpretují jako tzv "znaménková (signed)", tj namísto 0, 1, 2, 3, 4, 5 je to 0, 1, 2, -3, -2, -1. No a je celkem zřejmé, že pro sčítání záporných čísel platí to samé co pro sčítání kladných).
Offline
#43 30. 08. 2018 08:24 — Editoval vanok (30. 08. 2018 15:41)
Re: Realne matice
Ahoj ↑ MichalAld:,
Vidim, rozmyslas o tych grupach.
Mozno by ti pomohol pojem «delitela nuly »
Tak modulo 6, mas napr. 4*3=0. Povieme, ze 3 a aj 4 su delitelia nuly.
Akoze, chces najprv trocha prehlbit trochu tvoje znalosti o grupach, tak ( neskolskom neporiadku) ti sa pokusim tento pojem priblizit a az potom sa vratim ku grupam matic.
Tiez je uzitocne poznas pojem jednotnoveho okruhu 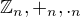 z operaciamy suctu a nasobenia modulo n ( ktore casto ak je jasne o co ide oznacim jednoducho
z operaciamy suctu a nasobenia modulo n ( ktore casto ak je jasne o co ide oznacim jednoducho 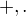 .
.
Poznamka. Ak praciujes napr modulo 6, tak skutocne mozes oznacit 0, 1,.. ,5 aj inymi reprezentantami ako 4=-2 a podobne. ( no to este ak treba upresnim).
A este, casto oznacim 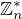 mnozinu invezibilnych prvkov mnoziny
mnozinu invezibilnych prvkov mnoziny  .
.
Na pokracovanie. Ak mas otazky, nevahaj.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#44 30. 08. 2018 16:48
Re: Realne matice
↑ vanok:
Ahojky.
Takže, dělitelé nuly, to je jasné.
Jednotkový okruh - jestli je to okruh s jednotkovým prvkem, jak je popsané třeba tady na wiki, tak tomu asi rozumím taky. Že existuje krom grupy ještě okruh a těleso, to jsem tak nějak věděl, ale co to je, to moc né.
Ta množina inverzibilních prvků - to se myslí invrzibilní k tomu násobení, že ?
Zkusím teda zjistit, pro naše modulo 5, které nejsou ty inverzibilní.
Pro násobení bude vypadat tabulka předpokládám takto:
0 1 2 3 4
-----------
0 | 0 0 0 0 0
1 | 0 1 2 3 4
2 | 0 2 4 1 3
3 | 0 3 1 4 2
4 | 0 4 3 2 1
Aby byl prvek inverzibilní, musí mít ve svém řádku nebo sloupci jedničku. To jsou v tomto případě, kromě nuly, všechny ostatní.
Dělitelé nuly tu naproti tomu žádné nevidím - což dává smysl, pokud je N prvočíslo.
Když vezmu modulo 4, tak:
0 1 2 3
---------
0 | 0 0 0 0
1 | 0 1 2 3
2 | 0 2 0 2
3 | 0 3 2 1
V tomto případě nejsou prvky 0 a 2 inverzibilní. A dvojka je dělitelem nuly.
Říkám to všechno správně ?
Offline
#45 30. 08. 2018 17:33 — Editoval vanok (30. 08. 2018 17:34)
Re: Realne matice
Servus ↑ MichalAld:,
Ano v podstate ano.
Pre nasobenie sa vyhodi ta nula.
A v pripade, ze n=p prvocislo tak skutocne dostanes teleso.
To je priklad konecneho komutativneho telesa.
Co sa tyka tvojho odkazu na cz vikipedii, tak tam najdes to najzakladnejsie. Ak chces trochu prehlbit, pozri napr. aj na anglicku a francuzku verziu, kde sa trochu viac poucis.
( I ked to ignoruje vela studentov tak existuju aj ine konecne telesa, no k tomu sa vratim neskor)
Tak upresnim teraz, este pojem  .
.
Ak chceme byt presny. Popisem ti podrobnejsie en pojem v pripade  .
.
Je jasne, ze zvysok 0 po delini cislom 5, maju cisla
...,-15,-10,-5,0,5,10,15,... a mnozinu takych cisiel oznacime 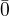
Podobne 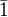 oznacit mnozinu cisiel ktore daju zvysok 1, po deleni cislom 5. : cize ide o mnozinu
oznacit mnozinu cisiel ktore daju zvysok 1, po deleni cislom 5. : cize ide o mnozinu  .
.
Povieme, ze je to trieda (klasa) cisla 1.
A podobne pre ine triedy. (Presnejsie ide o triedy ekvvivalencie.)
A tak mozme uvazovat, ze na  su operacie na takych klasach ( to aby bolo jasne o ake scitanie, ci nasobenie ide).
su operacie na takych klasach ( to aby bolo jasne o ake scitanie, ci nasobenie ide).
Este pripomeniem, ze miesto  . piseme tiez
. piseme tiez 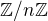 .
.
Na pokracovanie ( dufam, ze ta to stale bavi), kde nieco upresnim o tych generatoroch.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#47 31. 08. 2018 12:08 — Editoval vanok (01. 09. 2018 23:55)
Re: Realne matice
Ahoj ↑ MichalAld:,
Neboj sa, ja som tiez dost trpezlivy.
Mame takuto vetu:Veta 1
Nech 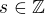
Nasledujuce tri vyroky su ekvivalentne.
a) s a n su nesudelitelne,
b)  je generator grupy
je generator grupy  ,
,
c)  ( grupy irverzibilnych prvkov pre nasobenie okruhu
( grupy irverzibilnych prvkov pre nasobenie okruhu  )
)
To tu dokazem.
No najprv male cvicenie
mozes urcit grupu inversibilnych prvkov pre n=2, 3,..., 10?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#48 31. 08. 2018 12:43
Re: Realne matice
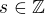
Jen se chci ujistit - to Z je tedy množina celých čísel, s, je tedy nějaké libovolné celé číslo, a Zn je je ta množina čísel v grupě modulo n ?
"nedudělitelné" znamená nesoudělné ?
Offline
#49 31. 08. 2018 13:16 — Editoval vanok (31. 08. 2018 13:23)
Re: Realne matice
Ahoj ↑ MichalAld:,
Mas pravdu.
A ten preklep opravim.
Pripominam.
Dve cele cisla su nesudelitelne,ak ich spolocne delitele su len 1 a -1 .
Edit.
V dokaze pouzijem aj https://cs.m.wikipedia.org/wiki/Bézoutova_rovnost .
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#50 31. 08. 2018 16:20
Re: Realne matice
vanok napsal(a):
Ahoj
No najprv male cvicenie
mozes urcit grupu inversibilnych prvkov pre n=2, 3,..., 10?
Nevím, jestli je na to nějaký elegantní trik. Jediné, co mě napadlo, že pokud jsou dva prvky (a, b) inverzibilní,
musí mezi nimi platit a.b =1, což v našem případě modulového dělení znamená, že mezi nimi musí být vztah
a.b = kN + 1. A z toho už se dá poznat, které prvky to splňují.
Takže pro jednotlivá N:
(0 nebude inverzibilní nikdy, 1 asi vždycky, sama se sebou)
N=2: a.b = 1 nebo 3 - žádný z prvků není inverzibilní
N=3: a.b = 1 | 4 => 2
N=4: a.b = 1 | 5 | 9 => 3
N=5: a.b = 1 | 6 | 1 | 16 => 2, 3, 4
N=6: a.b = 1 | 7 | 13 | 19 | 25 => 5
N=7: a.b = 1 | 8 | 15 | 22 | 29 | 36 => 2, 4, 3, 5, 6
N=8: a.b = 1 | 9 | 17 | 25 | 33 | 41 | 49 => 3, 5, 7
N=9: a.b = 1 | 10 | 19 | 28 | 37 | 46 | 55 | 64 => 2, 5, 4, 7, 8
N=10: a.b = 1 | 11 | 21 | 31 | 41 | 51 | 61 | 71 | 81 => 3, 7, 9
Doufám, že to mám dobře. Vlastně to odpovídá tomu, co jsi napsal, že inverzibilní čísla musí být nesoudělná s N.
Offline
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Realne matice
