Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 11. 2018 11:00
- Vecerrov

- Příspěvky: 26
Pravidelný devítiúhelník
Prosím o pomoc s úlohou z Petákové (je to strana 88, cvičení 52):
Je dán pravidelný devítiúhelník ABCDEFGHI. Vypočítejte:
a) velikost úhlů v trojúhelníku ACD
b) odchylku přímek BD, CI
Zatím mám toto:
Rozdělila jsem devítiúhelník na 9 pravidelných rovnoramenných trojúhelníků. Prostředek úhelníku jsem si označila S. Kolem S je úhel celkem 360°.
360°:9 = 40°. "Horní" úhel každého trojúhelníku je tedy 40°. Jelikož je trojúhelník rovnoramenný, zbývající dva úhly jsou shodné (180°-40°=140°/2=70°).
Teď ale nevím s těmi úhly v trojúhelníku ACD. Dohromady musí mít vnitřní úhly 180°. Kolik má který ale nevím.
S těma odchylkama přímek si už vůbec nevím rady...
Předem děkuji za odpovědi!
Offline
#2 11. 11. 2018 12:42
#3 11. 11. 2018 13:03 — Editoval Vecerrov (11. 11. 2018 13:04)
- Vecerrov

- Příspěvky: 26
Re: Pravidelný devítiúhelník
Děkuji.
Takže mi vyšlo tohle: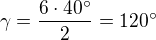

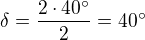
Doufám, že je to správně, mám jenom kopii strany z učebnice ale ne výsledky.
Teď ještě to b)....
Offline
#4 11. 11. 2018 13:48
Re: Pravidelný devítiúhelník
↑ Vecerrov:
Hodnoty jsou správně, a pokud je alfa u A, tak to je také dobře.
Adb) označím P jako průsečík těch přímek. Spočítej úhly v troj. DBC a IBC - opět obvodové a středové- a pomocí nich urči některý z úhlů u P.
Offline
#5 11. 11. 2018 19:15
- Vecerrov

- Příspěvky: 26
Re: Pravidelný devítiúhelník
Ano, alfu mám u A, gamu u C a deltu u D.
To b) nechápu... Jak mám z těch trojúhelníků zjistit úhel P?
Offline
#6 11. 11. 2018 19:54 — Editoval Al1 (11. 11. 2018 20:00)
Re: Pravidelný devítiúhelník
↑ Vecerrov:
Když budeš znát v troj. BCD vnitřní úhel u B a v troj. BIC vnitřní úhlu u C, spočítáš snadno úhel u P v troj. BCP.
Nezapomeň, že odchylka by měla mít velikost od 0 do 90 st.
Offline
#7 13. 11. 2018 16:19
- Vecerrov

- Příspěvky: 26
Re: Pravidelný devítiúhelník
Bohužel, nevím.. Nešel by napsat přesný postup?
Offline
#8 13. 11. 2018 17:04
#10 13. 11. 2018 18:28
#11 13. 11. 2018 18:39
- Vecerrov

- Příspěvky: 26
Re: Pravidelný devítiúhelník
Takže středový bude u P? Ten potřebuju, že...
K němu obvodové u B a C? Ale když neznám ani jeden ze tří úhlů... :-(
Offline
#12 13. 11. 2018 18:52 — Editoval Al1 (13. 11. 2018 18:55)
Re: Pravidelný devítiúhelník
↑ Vecerrov:
Obvodový úhel u B v troj. BCD - spočítej jako v případě a)
Obvodový úhel u C v troj. BCI - dpočítej jako a)
V troj. BCP je součet velikosti vnitřních úhlů 180°. Stačí dopočítat úhel u P.
Bod P neleží na kružnici, nemůžeš s ním počítat jako s obvodovým.
Offline
#14 13. 11. 2018 19:15 — Editoval Al1 (13. 11. 2018 19:15)
Re: Pravidelný devítiúhelník
↑ Vecerrov:
Opět počet dílků.
V troj. BCD je obvodový úhel CBD polovinou středového konvexního úhlu DSC, kde S je střed kružnice opsané devítiúhelníku. Úhel DSC je jeden díl, tedy 40°, obvodový je tedy jeho polovina.
Offline
#15 13. 11. 2018 19:43 — Editoval misaH (13. 11. 2018 19:44)
- misaH
- Příspěvky: 13460
Re: Pravidelný devítiúhelník
No - tých 20° sa dá veľmi jednoducho zistiť z rovnoramenného trojuholníka BCD.
Uhol BCD je vnútorný uhol toho 9-uholníka, má teda 2x70°=140°. (Vyplýva to z tých malých "dielikov", rovnoramenných trojuholníkov.)
Potom napríklad uhol CBD má (180-140):2 = 20 stupňov.
Offline
#16 13. 11. 2018 19:58 — Editoval misaH (13. 11. 2018 22:12)
- misaH
- Příspěvky: 13460
Re: Pravidelný devítiúhelník
Lichobežník ABCI má pri B aj A uhol veľký 140°, lebo je to vnútorný uhol v pravidelnom 9-uholníku. Lichobežník je rovnoramenný a teda sa dá vyrátať jeho uhol BCI (súčet v 4-uholníku je 360°).
Tým dostaneš ten uhol 40°.
No a uhol BPC sa už zistí jednoducho...
Pozor, že otázka je na uhol susedný, ktorý je ostrý. Z dvoch uhlov ktoré vytínajú rôznobežky je uhol medzi nimi ten ostrý a nie tupý.
Vďaka "kolegovi" Al1 za obrázok... :-)
Offline

