Matematické Fórum

jarrro · 14. 11. 2018 00:31 — Editoval jarrro (15. 11. 2018 18:46)

Ahoj.
Existuje v priestore so skalárnym súčinom nad reálnym poľom (prípadne ak by to niečo zmenilo tak Hilbertovom) taká báza, že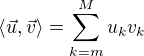
$\left\langle \vec{u}, \vec{v}\right\rangle=\sum_{k=m}^{M}{u_kv_k}$
Kde $\vec{u}=\sum_{i\in I}{u_i\vec{b}_i},\vec{v}=\sum_{j\in I}{v_j\vec{b}_j}\nl m=\min{$\min{\(I$},\min{$J$}\)},M=\max{$\max{\(I$},\max{$J$}\)}$ ?
Pre konečné dimenzie to (asi ) platí, lebo všetky s rovnakou dimenziou sú izomorfné
Platí to (existencia dobrej bázy) aj pre nekonečnorozmerné priestory?

Matematické Fórum

#1 14. 11. 2018 00:31 — Editoval jarrro (15. 11. 2018 18:46)

Existencia "kompatibilnej" bázy v priestore so skalárnym súčinom

Zápatí