Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#6 19. 11. 2018 17:08 — Editoval Flaky (19. 11. 2018 17:13)
Re: Upravení výrazu s mocninami a odmocninami
Zdravím,
postupoval přesně tak, jak bylo psáno, tj si jak v čitateli, tak ve jmenovateli vyjádřil u každého  příslušný exponent a použil pravidla pro práci s exponenciálou, jmenovitě
příslušný exponent a použil pravidla pro práci s exponenciálou, jmenovitě  a
a  a
a  .
.
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
#9 22. 11. 2018 16:06
Re: Upravení výrazu s mocninami a odmocninami
↑ Zakara:
Bohužel. Máš to chybně. Jen ses snažil přizpůsobit výpočet výsledku. Už za prvním rovnítkem je chyba ve jmenovateli. Platí totiž ![kopírovat do textarea $\sqrt[6]{\frac{1}{t^{-4}}\cdot \sqrt{t}}=\sqrt[12]{\frac{1}{(t^{-4})^{2}}\cdot t}$](/mathtex/95/95f21ffb3e478fd5c653c2b6e289ac49.gif) .
.
Další chyba je zkrácení odmocniny tvým způsobem, a i kdyby to šlo, pak  .
.
Za třetím rovnítkem máš chybně opsaného jmenovatele, s minusem nelze nakládat tak, že ho prostě vynecháš.
Také  , ale to už počítat je zbytečné, když si navršil tolik chyb.
, ale to už počítat je zbytečné, když si navršil tolik chyb.
Tak to zkus znovu.
Offline


![kopírovat do textarea $\sqrt[12]{t}=t^{\frac{1}{12}}$](/mathtex/38/38ae1936deebdd9aa6cac6ca47a88e80.gif) a pracuj již jen s exponenty základu t. Nezapomeň na podmínky.
a pracuj již jen s exponenty základu t. Nezapomeň na podmínky.
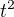



 , tak se pokračuje dál, jak jsi napsal. :-)
, tak se pokračuje dál, jak jsi napsal. :-)