Matematické Fórum

zzzz1 · 22. 11. 2018 07:15

Ahoj,
potřebuji poradit s tímto problémem.
$\text{Kolika způsoby lze rozdělit N čísel do pěti přihrádek} \\ \text{ tak aby žádná přihrádka nebyla prázdná a žádná} \\ \text{ dvě zasebou jdoucí čísla nebyla v téže přihrádce?}$

Vím, že počet způsobů jak rozdělit N čísel do pěti přihrádek je 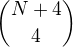${N+4 \choose 4}$ ale nevím jak spočítat počet těch s prázdnou přihrádkou nebo dvěma po sobě jsoucími čísly v jedné přihrádce.

Jj · 22. 11. 2018 09:34

↑ zzzz1:

Hezký den.

Prázdné přihrádky lze obvykle eliminovat tak, že se nejdříve do každé vloží jedno číslo a ke každé pětici takto vybraných čísel se přiřadí počet způsobů, jak rozdělit (N - 5) čísel do pěti přihrádek.

K druhé podmínce mě nic nenapadá.

Brano · 22. 11. 2018 11:10 — Editoval Brano (22. 11. 2018 11:11)

treba si navrhnut nejaky sposob ako ich budes delit do skatuliek

najprv urobme jednoduchsiu ulohu - ze ich delis do najviac 5 skatuliek t.j. ze niektore mozu byt aj prazdne
ako to budeme robit? mame gulicky ocislovane od 1 po N a budeme na ne lepit stitky s cislami 1 az 5 ktore reprezentuju skatulku do ktorej patria.
na jednotku mame 5 moznosti, na dvojku iba 4 moznosti, lebo nemoze byt v tej istej skatulke ako jednotka .. a dalej mame uz stale iba 4 moznosti
teda spolu 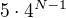$5\cdot 4^{N-1}$ moznosti

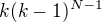keby sme tych skatuliek mali $k$ , tak by to bolo $k(k-1)^{N-1}$ - na to aby sme vylucili prazdne skatulky mozme pouzit princip inkluzie a exkluzie - skus sama a napis co dostanes