Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 12. 2018 15:41
- stuart clark

- Příspěvky: 1015
- Reputace: 7
number of quadrilateral
 is a convex quadrilateral with
is a convex quadrilateral with  and
and  points marked on its sides
points marked on its sides  and
and 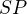 respectively.
respectively.
Triangles are formed using these 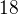 points and the original vertices of a quadrilateral.
points and the original vertices of a quadrilateral.
Then number of such triangle that do not have any side or part of a side common with the quadrialeral are
Offline
#2 08. 12. 2018 20:42
- check_drummer

- Příspěvky: 4896
- Reputace: 105
Re: number of quadrilateral
↑ stuart clark:
Hi, it seems that all triangles are part of the quadrilateral so the answer is 0. But maybe you mean not quadrilateral but its circumference, do you? If it is so what do you mean by "part" - when one point is common with that circumference is it part of it or not? May be you mean part that is of nonzero length...
"Máte úhel beta." "No to nemám."
Offline
#3 08. 12. 2018 21:11 — Editoval vanok (08. 12. 2018 21:12)
Re: number of quadrilateral
FHi ↑ stuart clark:,
The vertices of the triangles searched are selected in three sides of the quadrilateral  .
.
So the number of triangles with vertices on side is
3.4.5+3.4.6+3.5.6+4.5.6=...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 09. 12. 2018 13:14
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: number of quadrilateral
↑ check_drummer: actually question written in that language.
↑ vanok: can you please explain me in detail. Thanks
Offline
#5 09. 12. 2018 13:38
Re: number of quadrilateral
↑ stuart clark:,
For example,
The number of triangles with vertices on side  :
:
3 possibilities of vertices on side 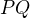
4 possibilities of vertices on side 
5 possibilities of vertices on side  ,
,
so you have 3.4.5 such triangles.
.... ( you have 3 others cases)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline