Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 12. 2018 20:01
Kladny polynom
Pozdravujem,
Nech  je kladny realny polynom stupna
je kladny realny polynom stupna  .
.
A nech 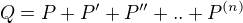 .
.
Dokazte, ze 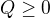 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 09. 12. 2018 02:23
#3 09. 12. 2018 03:52 — Editoval vanok (09. 12. 2018 08:16)
Re: Kladny polynom
Hi ↑ laszky:,
Celkom dobra praca.
Len by som doplnil, ze na zaciatok, treba ukazat : 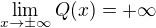 , lebo
, lebo  pre
pre 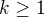 .
.
Poznamka: taketo cvicenia, kde mat dobre myslienky ti iste robia radost, ked ich vyriesis. Ze.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

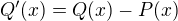 , plati
, plati  , takze v bodech, ve kterych ma polynom
, takze v bodech, ve kterych ma polynom  lokalni minimum plati
lokalni minimum plati  . Jedno z techto lokalnich minim je zaroven globalnim minimem, nebot polynom
. Jedno z techto lokalnich minim je zaroven globalnim minimem, nebot polynom